Simularea proceselor economice - problema de stocuri

Enuntul problemei

Firma B&C Center Links desfasoara activitatea de stocare , in care cererea zilnica este o variabila aleatoare discrete cu urmatoare distributie, stabilita pe baza unui studiu statistic:

X : ((50@0,20)(100@0.25)(150@0.25)(200@0,20)(250@0,10))

Ca prima ipoteza vom presupune ca cererea se satisfice la inceputul fiecarei zile.

Reaprovizionarea se face la diferite interval de timp, perioada de timp dintre momentul lansarii unei comenzi si intrarea marfii in stoc, durata de reaprovizionare, este tot o variabila aleatoare de tip discret de forma:

Y : ((3@0,20)(4@0,40)(5@0,30)(6@0,10))

Activitatea de stocare presupune urmatoarele cheltuieli:

-cheltuieli de stocare, cs=10 um/buc/zi;

-cheltuieli de lansare a unei comenzi de reaprovizionare, cl=4000 um;

Cheltuieli de penalizare in cazul lipsei de stoc, cp=60 um/buc/zi;

Stocul initial este S0=500 buc.

Cererile ce nu pot fi satisfacute din stocul current se pastreaza urmand a fi satisfacute in zilele urmatoare. Activitatea de stocare este avantajoasa daca se desfasoara in conditiile unor cheltuieli totale minime.

Pe baza acestor elemente sa se construiasca un algorimt de simulare in vederea adoptarii uneia din urmatoarele doua politici de gestiune a stocului:

P1: comanda de reaprovizionare se lanseaza in momentul in care nivelul stocului atinge un nivel de alarma Na=400 buc. Cantitatea cu care se face reaprovizionarea este fixa, Q=700 buc. O noua comanda nu se poate lansa cand vechea comanda nu este primita.

P2: reaprovizionarea se face regulat, o data la 5 zile, cu cantitatea ceruta in ultimele 5 zile. In prima zi se lanseaza o comanda de reaprovizionare Q=500 buc.

P3: reaprovizionarea se face regulat, o data la 6 zile, cu o cantitate fiza Q=800 buc. In prima zi se lanseaza o comanda de reaprovizionare Q=800 buc.

Orizontul de simulare pentru toate politicile este O=20 zile.

Pregatirea simularii

Scop: cheltuieli totale minime.

Variabile de intrare: constante(cheltuieli de stocare, cheltuieli de lansare,cheltuieli de penalizare,etc)

Variabile aleatoare:

Cererea:

X: ((x_i@λ^(x_i )/(x_i !) e^(-λ) ))xi є N

x є Po (λ) , λ=cererea medie zilnică

M(x)= λ, D(x)=λ;

Durata de reaprovizionare:

Y: ((y_i@λ^(y_i )/(y_i !) e^(-λ) ))yi є N

y є Po (λ) , λ=durata medie de reaprovizionare

M(y)= λ, D(y)=λ;

Variabile de iesire: cheltuieli totale minime.

Simluarea cererii si a duratei de reaprovizionare

Cererile zilnice si duratele de reaprovizionare vor fi simulate prin metoda transformatei inverse.

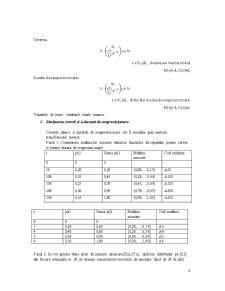
Pasul 1: Construirea multimilor asociate valorilor functiilor de repartitie pentru cerere si pentru durata de reaprovizionare:

r p(r) Suma p(r) Multimi asociate Cod multime

0 0 0 - -

50 0,20 0,20 {0,00;.;0,19} A50

100 0,25 0,45 {0,20;.;0,44} A100

150 0,25 0,70 {0,45;.;0,69} A150

200 0,20 0,90 {0,70;.;0,89} A200

250 0,10 1,00 {0,90;.;1,00} A250

t p(t) Suma p(t) Multimi asociate Cod multime

0 0 0 - -

3 0,20 0,20 {0,00;.;0,19} A3

4 0,40 0,60 {0,20:.:0,59} A4

5 0,30 0,90 {0,60:.:0,89} A5

6 0,10 1,00 {0,90;.;1,00} A6

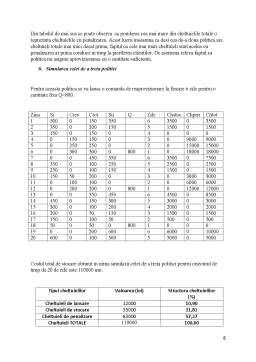
Pasul 2: Se vor genera doua siruri de numere aleatoare(Xn),(Yn), uniform distribuite pe [0,1] din fiecare retinandu-se 20 de termini consecutive(orizontul de simulare fiind de 20 de zile).

In tabelul urmator se evidentiaza apartenenta valorilor generate ale sirurilor (Xn) si (Yn) la multimile asociate, precum si valorile corespunzatoare ale cererilor simulate(r) si respectiv, duratelor de reaprovizionare simulate(t).

De exemplu, prima valoare retinuta din sirul (Xn) este X1=0,92 care apartine multimii associate cu codul A250 si prion urmare cererea primei zile va fi r1=250,respective, prima valoare retinuta din sirul (Yn) este Y1=0,67 care apartine multimii associate cu codul B5, care semnifica faptul ca prima comanda va intra in stoc dupa o perioada de timp de t=5 zile.