Cuprins
- NOTIUNI GENERALE 4
- I. REDUCTOR CONIC CU DINTI DREPTI 7
- 1.1.Reductoare,cu o singura treapta de reducere 7
- 1.2 Variante Constructive 8
- 1.3.Justificarea variantei alese 13
- 1.4. Intretinerea dispozitivului 13
- 1.5 Montarea rotilor 13
- II. MEMORIUL JUSTIFICATIV DE CALCUL 14
- 2.1 Calculul angrenajului conic 14
- 2.2. Calcul raport de transmitere roti conice. 14
- 2.3. Se calculeaza turatiile pe fiecare arbore 14
- 2.4. Se calculeaza Puterile pe fiecare arbore 15
- 2.5. Calculul momentelor de torsiune 15
- 2.6 Calculul gradului de acoperire al angrenajului conic si al Randamentului 16
- 2.7. MechSoft 2004 16
- 2.8. Raport MechSoft al angrenajului conic 37
- III.TRANSMISIA PRIN CURELE 41
- 3.1 Dimensionare roti de curea 45
- 3.2 Fixarea pieselor pe capetele de arbore 51
- IV.CALCULUL ARBORILOR 52
- 4.1 Dimensionare capat de arbore pinion conic 53
- 4.2 Dimensionare capat arbore de iesire 54
- 4.3 Forte rezultate din angrenajul conic 55
- 4.4. Calculul reactiuni arbore de intrare 57
- 4.5 Calculul reactiuni arbore de iesire 59
- 4.6 Verificare reactiuni pinion conic 61
- 4.7 Verificare reactiuni arbore de iesire 75
- 4.8 Calculul penelor 85
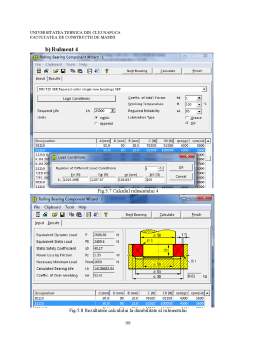
- V. Rulmenti 91
- 5.1 Calculul Rulmenti pinion.Montaj in O 91
- 5.2 Calcul rulmenti arbore iesire 97
- VI. Carcasa reductor 101
- VIII.Lubrifianti 106
- 8.1 Verificarea la incalzire a reductorului 106
- Bibliografie 107
Extras din proiect
NOTIUNI GENERALE
Angrenajele conice sunt angrenaje cu axe concurente la care suprafeţele de rostogolire au formă conică şi sunt tangente după o generatoare comună, iar suprafeţele exterioare ale roţilor componente au aceeaşi formă ca şi suprafaţa de rostogolire, adică suprafeţe conice.
Între axele suprafeţelor de rostogolire şi generatoarea comună se stabilesc unghiurile, unghiuri a căror sumă reprezintă unghiul între axele de transmitere a mişcării, unghi notat ∑.
In cazul în care unul din aceste unghiuri este de 90o, conul respectiv se transformă într-o suprafaţă plană, dantura fiind înscrisă într-un cerc pe această suprafaţă. Angrenajul capătă în această situaţie denumirea de angrenaj conic cu roată plană.
Roata plană în angrenajul conic corespunde cremalierei din angrenajul cilindric, ea fiind intermediară între roata conică cu dantura exterioară şi cea cu dantura interioară.
Din punct de vedere geometric, dantura angrenajului conic corespunde unor suprafeţe conjugate definite conform teoriei angrenării, dar studiul acestor suprafeţe pune o serie întreagă de probleme a căror rezolvare nu se face absolut exact din punct de vedere matematic, ci folosind o serie de aproximaţii pentru a se stabili o metodologie de calcul mai larg accesibilă şi, totodată, pentru asigurarea posibilităţii de execuţie. Din punct de vedere cinematic, problema care se pune este de a determina prin calcul dimensiunile danturii şi limitele între care există posibilitatea de generare a suprafeţelor conjugate ale dinţilor. Acest studiu al angrenajului conic prezintă o serie de dificultăţi, dat fiind faptul că suprafeţele de rostogolire (axoidele) sunt suprafeţe conice şi că cele două cercuri de rostogolire ale bazei axoidelor nu se găsesc în acelaşi plan (fig.2).
Datorită acestui fapt nu se poate aplica direct teoria angrenării, dezvoltată pentru angrenarea în plan, în vederea determinării caracteristicilor danturii. Evident, prin metodele geometriei diferenţiale este posibil studiul teoretic al acestui tip de angrenare, dar relaţiile de calcul sunt complicate, ceea ce nu le conferă o utilitate imediată fără programe de calcul foarte bine puse la punct.
O altă cale de studiu a fost ca, prin analogie cu angrenarea în plan, să se dezvolte o geometrie a angrenării teoretic exactă, plecând de la încadrarea suprafeţelor conice într-o sferă şi aplicând formulele trigonometriei sferice (fig.3), profilul dintelui roţilor conice rezultând după o evolventă sferică.
Dintele roţii plane obţinute în acest caz nu are însă profil rectiliniu, ci unul cu punct de inflexiune, ceea ce reprezintă complicaţii constructive în ceea ce priveşte realizarea sculelor (fig.4).
Toleranţele pentru angrenajele conice sunt stabilite prin STAS 6460-61; ele se aplică la angrenaje conice concurente cu roţi dinţate metalice prelucrate, cu dinţi drepţi, înclinaţi sau curbi, având diametrul de divizare până la 2000mm şi modulul exterior de la 1 până la 30mm.
Sunt prevăzute 12 clase de precizie, fără a prevedea toleranţe pentru clasele de precizie 1, 2, 3, 4 şi 12.
Fiecare clasă de precizie este determinată de criteriile de precizie cinematică a roţii, de funcţionarea lină în angrenare, de contactul dintre dinţi.
Fiecare criteriu de precizie este caracterizat prin anumite erori şi abateri ale elementelor roţilor dinţate conice şi a angrenajelor, denumite indici de precizie.
În alegerea criteriilor de precizie se admite şi combinarea lor, având toleranţe din diferite clase de precizie, respectându-se unele reguli. Astfel, criteriul de funcţionare lină nu poate să difere decât cu o clasă de precizie în sus sau în jos faţă de criteriul de precizie cinematică.
Criteriul de contact dintre dinţi nu poate fi de clasă mai puţin precisă decât clasa de precizie a criteriului de funcţionare lină a roţii în angrenaj.
Forma dinţilor :
• Roţi plane cu dinţi ale căror flancuri sunt plane
• Roţi conice cu dinţi drepţi (cremalieră circulară cu dinţi drepţi)
• Roţi conice cu dinţi înclinaţi (cremalieră circulară cu dinţi înclinaţi)
• Roţi conice cu dinţi curbi (cremalieră circulară cu dinţi curbi).
Funcţiunea
Angrenajul cu roţi conice transmite puterea nominală P1n de la un arbore conducător (1) cu turaţia n1 la un arbore condus (2) cu turaţia n2, axele celor doi arbori fiind concurente (în general, unghiul axelor este de 90o).
Contactul perfect şi rigid între dinţii unui angrenaj conic cu dinţi drepţi sau înclinaţi, al cărui cremalieră circulară are flancurile plane, se face după o dreaptă; între dinţii curbi, contactul perfect şi rigid se face după o curbă.
Roata (1) acţionează asupra roţii (2) prin forţe normale şi tangenţiale faţă de flancurile dinţilor în contact, repartizate de-a lungul contactului. Repartizarea este proporţională cu deformaţiile elastice ale dinţilor în contact, care variază proporţional cu distanţa până la vârful comun al conurilor primitive; rezultă o repartizare trapezoidală a forţelor normale şi tangenţiale pe lungimea contactului. Rezultantele Fn şi µFn¬ ale acestor forţe sunt aplicate într-un punct deplasat spre periferia roţilor faţă de punctul median. Direcţia acestor forţe variază de-a lungul arcului de angrenare descris de punctul lor de aplicaţie. În calculele obişnuite se consideră, cu o aproximaţie neglijabilă, că punctul de aplicaţie se găseşte în mijlocul liniei de contact şi se neglijează variaţia orientării.
Caracteristici
Angrenajul cu roţi conice este mai scump decât angrenajul cu roţi cilindrice. Prelucrarea şi montajul trebuie să fie supravegheate mai atent. Din cauza greşelilor de montaj, a prelucrării sau a deformaţiei în funcţionare, se produce o deplasare a vârfurilor conurilor primitive; contactul rigid devine punctual, cel real (elastic) se produce într-o zonă în vecinătatea punctului de contact rigid; se produc concentrări de sarcini, vibraţii şi zgomot. Pentru corectarea acestor erori inevitabile, dinţii se fac bombaţi, ca şi la angrenajele cilindrice.
Domenii de aplicare
Se folosesc în construcţia de maşini, unde este nevoie să se transmită mişcarea între doi arbori concurenţi (cel mai des între doi arbori care fac între ei un unghi de 90o).
Roţile conice cu dinţi drepţi se folosesc pentru viteze periferice mici (2...3m/s); la viteze mai mari se folosesc roţile cu dinţi curbi, asigurând un mers mai liniştit. Se folosesc în mod obişnuit pentru rapoarte de transmitere până la i = 6.
La maşinile de danturat roţi conice, muchia cuţitului de tăiat se mişcă în poziţia finală, de-a lungul flancului dintelui cremalierei circulare, materializând astfel acest flanc. Roata conică execută mişcarea relativă de rostogolire faţă de cremaliera circulară. Se obţine astfel flancul dintelui roţii conice ca înfăşurătoare a flancului dintelui cremalierei. Se pot obţine roţi conice cu cremaliera circulară deplasată faţă de poziţia normală. Spre deosebire de angrenajele cilindrice, nu se pot obţine decât angrenaje conice de zero
Bibliografie
1.Ovidiu Tataru ,Adalbert A,Ovidiu B Lucian T, Stefan B,s.a-”REDUCTOARE”-reeditare 1994 [1]
2.Ovidiu Belcin,Corina Birleanu, Marius Pustan-“ORGANE DE MASINI” , Editura Risoprint 2011 [2]
3.Dumitru Pop, Lucian Tudose, Simion Haragas-“LAGARE CU RULMENTI” [3]
4.Ovidiu Tataru –Notite curs [4]
5. Simion Haragas- “reductoare cu o treapta” Editura Risoprint, 2014 [5]
Preview document
Conținut arhivă zip
- Calcule .xmcd
- Calcule Angrenaj .cal
- Calcule Angrenaj 1.cal
- Calcule Reactiuni .xmcd
- Calcule roata curea .cal
- Dimensionare arbore iesire .cal
- Dimensionare arbore iesire v1.cal
- Dimensionare Pinion conic .cal
- Dimensionare Pinion conic v1.cal
- Raport angrenaj conic MechSoft.txt
- Raport transmisie prin curele SPZ.txt
- Reductor conic cu dinti drepti cu o treapta de turatie.docx
- Verificare pana A10x8x56.cal
- Verificare pana A12x8x70.cal
- Verificare pana A14x8x56.cal
- Verificare rulment 1.cal
- Verificare rulment 2.cal
- Verificare rulment 3.cal
- Verificare rulment 4.cal