Extras din referat
Cand auzim acest titlu prima oara, imaginea care ne apare in minte este un calculator de la NASA care codifica date confidentiale si zece mii de rusi care se chinuie sa le decodifice. De fapt, codificarea si decodificarea datelor are multe aplicatii, extinse in toata informatica: de la arhivatoare, pana la asigurarea securitatii datelor in transmiterea lor prin retea sau internet.
Haideti sa incepem cu arhivarea datelor, operatiune fara care multi nu si-ar putea imagina
Compresia datelor consta in transformarea unui “text” de intrare, in “cod”, intr-un fisier comprimat. Pentru a fi folositoare, o schema de compresie trebuie sa poata fi transformata din fisierul comprimat inapoi in fisierul text initial. Numai trebuie spus, ca ar fi bine ca fisierul comprimat sa fie mai mic decat cel initial.
Exista mai multi algoritimi de compresie, fiecare bazandu-se pe un principiu diferit. Vom exemplifica unele din acestea:
Sistemele de compresie bazate pe dictionare, inlocuiesc grupuri de simboluri (cuvinte) din textul initial, cu codificari de lungime prestabilita.Un exemplu elocvent al acestui tip de sistem este tehnica LZW, care inlocuieste siruri de caractere predefinite de lungime nelimitata, cu codificari pe 9-16 biti. Nu vom dezvolta aceasta tehnica, deoarece necesita o implementare migaloasa si de durata.
Metodele statistice de compresie abordeaza lucrurile complet diferit. Aceste codifica simbolurile pe rand, in ordinea in care sa gasesc acestea in text. Simbolurile sunt transformate in coduri de lungime variabila. Lungimea codificarii variaza in functie de frecventa (numarul de aparitii) simbolului. Cele cu frecventa mica sunt codificate pe mai multi biti, iar cele cu frecvanta mare, pe mai putini.
In practica, linia de diferentiere dintre cele doua metode nu este totdeauna foarte clara. Despre unele fisiere nu se poate spune ca se arhiveaza mult mai bine cu una din cele doua variante, de aceea exista tehnici care sunt un hibrid intre cele doua, dand astfel rezultate mult mai bune. In continuare, ne vom axa totusi doar pe codificarea aritmetica pentru a implementa o schema pur statistica.
Codificarea Huffman:
Nu este de ajuns sa putem calcula frecventa unui simbol intr-un fisier, avem nevoie si de o metoda prin care sa profitam de aceasta informatie. Probabil cea mai raspandita metoda de codificare bazata pe statistica este codificarea Huffman. D.A. Huffman a publicat o lucrare in 1952 in care descria o metoda de creare a unui tabel de codificare a simbolurilor tinand cont de frecventa acestora. Tabelul va produce sigur cel mai mic fisier de iesire posibil, folosind codificari de lungime fixa. Alte sisteme de codificare, cum ar fi Shannon-Fano, au fost demonstrate a fi non-optime.
Codificarea Huffman atribuie o codificare fiecarui simbol, rezultatele fiind de la 1 bit lungime pana la o codificare de lungime considerabil mai mare decat a simbolului initial, depinzand strict de frecventa acestuia. Numarul optim de biti care trebuie sa fie folositi este logaritmul in baza 2 din 1/p, unde p este probabilitatea de aparitie. Deci, daca probabilitatea aparitiei unui simblo este 1/256, cum ar fi de exemplu intr-un sir aleator de biti, atunci numarul optim de biti pentru fiecare caracter este log in baza 2 din 256 adica 8. Daca probabilitatea ajunge pana la 1/2, atunci numarul optimi de biti este 1.
Problema cu aceasta schema este ca numarul de biti folositi in codificare trebuie sa fie un numar intreg. Deci daca avem o probabilitate de 1/3 atunci numarul optim de biti ar fi 1.6. In acest caz trebuie ales ori 1 ori 2 biti pentru codificare si oricare alegere duce la o dimensiune de codificare mai mare decat cea teoretic posibila.
Sistemul Huffman mai are inca o mica problema. Odata cu fisierul codificat, trebuie transmisa si schema de codificare, pentru ca face decodificarea posibila. Aceasta se adauga la marimea fisierului final. Pentru aceasta problema exista o rezolvare partiala, numita metoda schemelor adaptate, pe care totusi nu o vom prezenta deoarece necesita cunostinte avansate de programare dinamica.
Codificarea Aritmetica: mod de functionare
Abia acum cca. zece ani s-a demonstrat o metoda care poate concura cu sistemul Huffman. Codificare aritmetica trece peste ideea de a inlocui un simbol cu un cod predefinit. In schimb, transforma un input cu un singur numar floating point. Cu cat e mai lung si mai complex mesajul (input-ul), cu atat mai multi biti se folosesc pentru reprezentarea numarului. Si totusi, abia recent s-a gasit o metoda practica de a implementa un asemenea sistem pe un calculator cu registrii de dimensiune fixa.
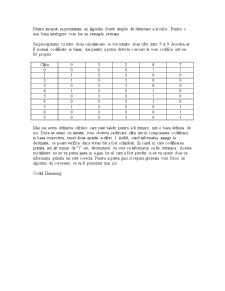
Iesirea (output-ul) unui astfel de proces este un singur numar intre 0 si 1. Acest numar poate fi decodat pentru a recrea mesajul initial. Pentru a crea fisierul final, simbolurile codificate trebuie sa aiba probabilitati asignate. De exemplu, daca am de gand sa codific mesajul “BILL GATES”, as avea o distributie a frecventelor dupa cum urmeaza:
Preview document
Conținut arhivă zip
- Codificarea si Decodificarea Datelor.doc