Cuprins
- 1 TEMA REFERATULUI 2
- 2 ASPECTE TEORETICE ALE FIABILITATII SOFTWARE 2
- 2.1 INDICATORI DE FIABILITATE 2
- 2.2 MODELE DE FIABILITATE 2
- 2.2.1 Modelul Jelinski-Moranda 2
- 2.2.2 Modelul Musa-Okumoto 3
- 2.2.3 Modelul Littlewood-Verall 3
- 2.3 SUPERMODELE 3
- 2.4 TESTAREA DATELOR 3
- 2.4.1 Media aritmetică a execuţiilor 4
- 2.4.2 Testul Laplace 4
- 2.4.3 Execuţia modelelor şi interpretarea rezultatelor 5
- 3 BIBLIOGRAFIE 15
Extras din referat
Fiabilitatea softurilor.
2 Aspecte teoretice ale fiabilităţii software
2.1 Indicatori de fiabilitate
Definiţie: Fiabilitatea unui program este probabilitatea ca sistemul din care face parte să opereze fără vreo defectare datorată activării unui defect în program, în condiţii date şi într-un interval de timp dat.
Indicatori:-Fiabilitatea “R(t)”
-Media timpurilor între defectări “MTTF”
-Mediana “m”
-Rata defectărilor “ ”
2.2 Modele de fiabilitate
Problema estimării fiabilităţii software este o problemă de predicţie, indicatorii prezentaţi anterior sunt încorporaţi într-o formă sau alta în aşa numitele modele de fiabilitate software (MFS) acestea sunt modele statistice ce realizează predicţii asupra ratei de defectare a unui program cunoscându-se istoria lui. Ele realizează şi ipoteze asupra procesului de depistare şi eliminare a erorilor.
Există două tipuri de MFS-uri care prezic timpul între defectări şi care prezic numărul de defectări într-un interval de timp dat.
Cele dim prima clasă pot fi exprimate ca o funcţie densitate de probabilitate ai cărei parametri pot fi estimaţi pe baza valorilor timpilor dintre defectele anterioare, această funcţie este utilizată pentru a previziona timpul până la următoarea defectare precum şi fiabilitatea sistemului software. Parametrii lui pot fi estimaţi fie prin metoda verosimilităţii maxime fie prin metoda celor mai mici pătrate.
În continuare vom prezenta cele mai importante trei modele de estimare a fiabilităţii software:
2.2.1 Modelul Jelinski-Moranda
Ipoteze:
a) Rata detecţiei defectelor este proporţională cu numărul curent de defecte din program.
b) Toate defectările au acela-şi probabilitate de apariţie şi sunt independente una de alta.
c) Fiecare defectare are acela-şi ordin de severitate.
d) Rata de defectare rămâne constantă în intervalul dintre două defectări.
e) Probramul este executat în manieră similară cu funcţionarea operaţională anticipată.
f) Defectele sunt corelate instantaneu fără introducerea în program a unor defecte noi.
g) Numărul total de defecte aşteptate este limitat superior.
Punctele slabe ale modelului:
- ipotezele iniţiale sunt aproximative.
- estimărilre parametrilor au priorităţi limitate.
- predicţiile de fiabilitate sunt optimiste.
2.2.2 Modelul Musa-Okumoto
Ipoteze:
a) Detecţiile defectărilor sunt independente unele de altele.
b) Numărul de defectări aşteptat este o funcţie de timp logaritmică.
c) Intensitatea de defectare scade exponenţial cu numărul aşteptat al defectărilor apărute.
d) Nu există o limită superioară a numărului total de defectări.
e) Probramul este executat în manieră similară cu funcţionarea operaţională anticipată.
Principalele caracteristici ale modelului sunt:
- foloseşte pentru rata defectărilor relaţia
- predicţia este realizată prin utilizarea unor estimări ale parametrilor.
2.2.3 Modelul Littlewood-Verall
Ipoteze:
a) Timpii între defectări consecutive sunt variabile aleatoare independente fiecare având o distribuţie exponenţială.
b) Rata de defectare formează o secvenţă de variabile independente fiecare din ele având o altă distribuţie. Cu alte cuvinte programul poate deveni mai puţin fiabil pe durata testării dacă în program sunt introduse mai multe defecte decât cele eliminate în etapa de corecţie.
c) Nu există o limitate superioară a numărului de defecte.
Avantaje:
- poate reprezenta incertitudinea depanării.
- poate reprezenta creşterea sau scăderea fiabilităţii.
Dezavantaje:
- nu poate estima numărul defectelor rămase.
2.3 Supermodele
Un supermodel se obţine prin combinarea unor modele de bază atribuind fiecăruiea o anumită pondere.
Pot fi definite trei tipuri de combinaţii:
1. Combinaţii liniare ponderate statistic
2. Combinaţii în care ponderile sunt atribuite dinamic pe baza comportării rezultatelor modelelor pe durata celor “n” observaţii anterioare.
3. Combinaţii în care ponderile sunt atribuite dinamic pe baza verosimilităţii previzionale asupra celor “n” observaţii anterioare.
2.4 Testarea datelor
Se poate demonstra că problema predicţiei fiabilităţii unui software are sens numai dacă setul de date indică o creştere în timp a fiabilităţii. Astfel există două metode care permit detectarea tendinţei de evolutie a fiabilităţii înainte de a începe analiza propriu-zisă a datelor.
2.4.1 Media aritmetică a execuţiilor
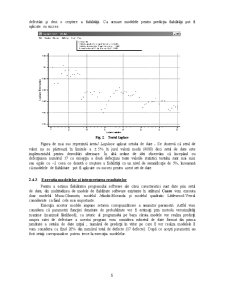
Rezultatele testului sunt afişate grafic şi sunt interpretate după cum urmează.Pentru datele timpi între defectări dacă media execuţiilor creşte atunci timpul între defectări creşte şi deci creşte şi fiabilitatea sistemului, prin urmare modelele pot fi aplicate dacă media aritmetică a execuţiilor este crescătoare.
Preview document
Conținut arhivă zip
- Fiabilitatea Softurilor.doc