Măsuri ale tendinței centrale, ale variabilității, ale dispersiei și ale poziției

Măsuri ale tendinţei centrale, ale variabilităţii, ale dispersiei şi ale poziţiei

Problematică:

REZULTATELE ALEGERILOR PREZIDENŢIALE, DIN 27 SEPTEMBRIE 1992

- primul tur de scrutin -

Introducere

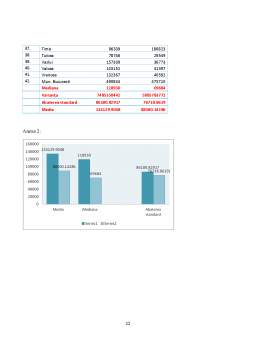
În cele ce urmează voi analiza numărul voturilor liber exprimate din cadrul alegerilor prezidenţiale, din data de 27 septembrie 1992(primul tur de scrutin); mai exact m-am oprit asupra voturilor domnului Ion Iliescu si cele ale domnului Emil Constantinescu. Plec de la ipoteza că în judeţele ţării, unde numărul de locuitori este mai mare ar trebui ca şi numărul voturilor să fie pe măsură.

Pentru a analiza această problematică voi folosi metoda de măsurare a tendinţei centrale, a variabilităţii, a dispersiei şi a poziţiei. Iar datele pe care le-am cules pentru a le analiza sunt sub forma unui tabel, existent pe site-ul Institutului Naţional de Statistică.

Capitolul I:

Descrierea teoretică a metodei de cercetare empirică utilizată în proiect

Cele mai multe dintre seturile de date arată o tendinţă clară a datelor de a se grupa în jurul unui punct central. Din acest motiv, pentru orice set de date, o anumită valoare tipică poate fi utilizată pentru a descrie întregul set. O astfel de valoare descriptivă se numeşte măsură a tendinţei centrale. Există trei astfel de măsuri ale tendinţei centrale: media aritmetică, mediana şi modul.

Media aritmetică

Media aritmetică reprezintă cea mai utilizată măsură a tendinţei centrale. Media aritmetică se calculează prin împărţirea sumei tuturor valorilor numerice ale unei variabile dintr-un set de date la numărul de date din acel set.

Pentru un eşantion care conţine n observaţii, notate X1, X2, , Xn, media aritmetică a eşantionului, notată şi numită X barat, se calculează după formula:

Pentru o populaţie care conţine N observaţii, media aritmetică a populaţiei se notează cu litera grecească μ şi se calculează după o formulă similară:

Trebuie subliniat faptul că μ reprezintă un parametru, iar este doar o informaţie statistică.

Proprietăţile mediei:

- media este o măsură potrivită doar pentru datele cantitative

- media este puternic influenţată de observaţiile care sunt foarte depărtate de restul datelor, care sunt numite observaţii excentrice.

Mediana

Mediana este măsura care împarte exact în două un şir ordonat de date.

Mediana = a (n+1)/2 observaţie.