Extras din document
Problema drumului de lungime minimă din orice vârf
-
Problema se referă la aflarea costului minim din orice vârf către oricare alt vârf, folosind muchii multiple
-
Aceasta se numește problema drumului de lungime minimă din orice vârf (all-pairs shortest path problem)
Algoritmul lui Floyd
-
Algoritmul lui Warshall reprezintă o modalitate rapidă de a crea un tabel care indică vârfurile în care se poate ajunge dintr-un anumit vârf, într-unul sau mai mulți pași
-
O abordare similară pentru grafuri ponderate este folosită de algoritmul lui Floyd, descoperit de Robert Floyd în 1962
Observații
-
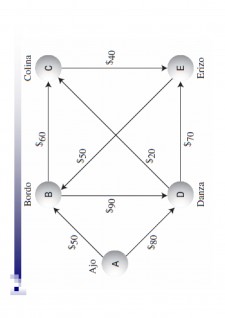
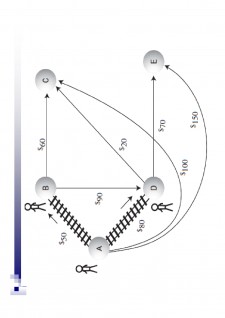
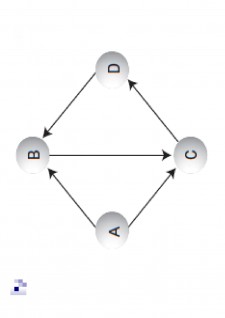
Matricea de adiacență indică costurile tuturor căilor cu o singură muchie
-
Se dorește extinderea acestei matrici pentru a indica costurile tuturor căilor, indiferent de lungimea lor
-
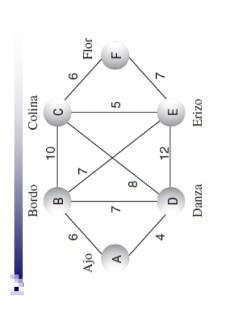
De exemplu, se poate ajunge de la B la C cu un cost de 30 (10 de la B la D și 20 de la D la C)
Observații
-
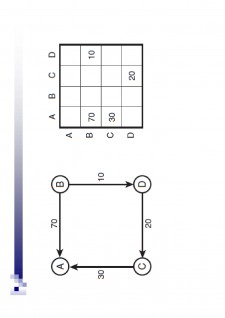
Similar algoritmului lui Warshall, se modifică matricea de adiacență
-
Se examinează fiecare celulă de pe fiecare rând
-
Dacă există o pondere pozitivă, de exemplu 30 la intersecția liniei C cu coloana A, atunci se analizează coloana C, deoarece C reprezintă linia unde se află 30
Observații
-
Dacă se găsește o celulă în coloana C, de exemplu 40 la linia D, atunci există o cale de la C la A cu o pondere de 30 și o cale de la D la C cu o pondere de 40
-
Se poate deduce că există o cale cu două muchii de la D la A, cu o pondere de 70
Observații
-
Linia A este vidă
-
Pe linia B este 70 în coloana A și 10 în coloana D, dar coloana B este vidă, deci muchiile care încep din B nu pot fi combinate cu nicio muchie care se termină în B
Observații
-
În linia C se află 30 pe coloana A
-
În coloana C se află 20 pe linia D
-
Muchia de la C la A are o pondere de 30
-
Muchia de la D la C are o pondere de 20
-
Se obține calea de la D la A cu ponderea de 50
Observații
-
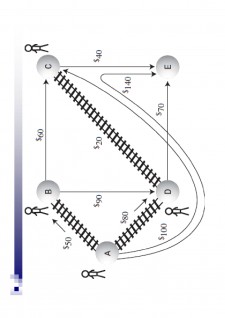
Linia D arată o situație interesantă - se poate micșora un cost existent deja
-
Pe linia D există 50 în coloana A
-
Pe linia B există 10 în coloana D
-
Există o cale de la B la A cu costul 60
-
Cu toate acestea, există deja costul 70 pe linia B, în coloana A
Observații
-
Deoarece 60 e mai mic decât 70, se înlocuiește 70 cu 60
-
În cazul căilor multiple de la un vârf la altul, tabelul indică calea de cost minim
Observații
-
Implementarea algoritmului lui Floyd este similară algoritmului lui Warshall
-
În locul inserării valorii 1 în tabel, cum se procedează în algoritmul lui Warshall, când se găsește o cale cu două muchii, se adaugă costul căii cu două muchii și se inserează suma costurilor celor două muchii în tabel
Preview document
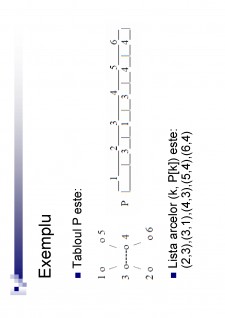
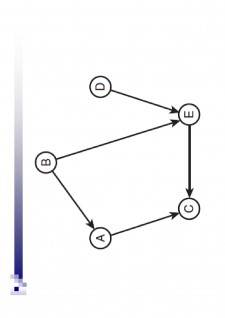
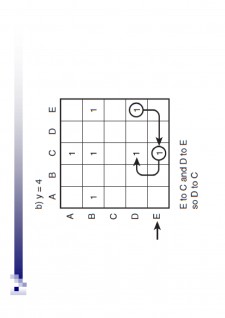
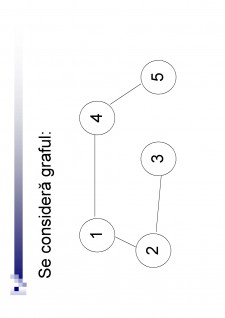
Conținut arhivă zip
- Algoritmul lui Floyd.pdf
- EXPLORAREA GRAFURILOR.pdf
- GRAFURI.pdf
- GRAFURI PONDERATE.pdf
- Grafuri Quiz 3.pdf
- Introducere in Teoria Grafurilor+Raspunsuri.pdf
- Quiz Grafuri 2.pdf
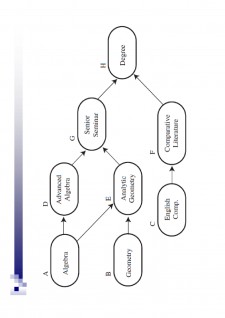
- SORTAREA TOPOLOGICA.pdf
Alții au mai descărcat și
Căpşunul este o plantă semiierboasă, perenă, ce creşte sub formă de tufă cu înălţimea de 15-40 cm. Partea subterană este formată dintr-o rădăcină...
BILANȚUL ENERGIEI LA NIVEL DE FERMĂ Energia reprezită capacitatea unui sistem de a efectua lucru mecanic, atunci când trece printr-o transformare...
ARHITECTURĂ TIPURILE DE SPAŢII VERZI Spaţiile verzi din interiorul localităţilor cuprind: parcuri, grădini, scuaruri, fâşii verzi şi aliniamente...
INTRODUCERE ÎN ŞTIINŢA POMICULTURII Valorificarea eficientă a condiţiilor ecologice, tehnologice şi social-economice de care dispune fiecare...
1.1. AMELIORAREA GRÂULUI Grâul este un aliment de bază care este principala sursă de hrana pentru aproximativ 40% din populaţie. Datorită...
INTRODUCERE Lintea face parte din ordinul Leguminosales. Importanţa ei constă în conţinutul ridicat de proteină al seminţelor (38 %)...
CURS 1 PREGĂTIREA MATERIILOR PRIME PENTRU PRELUCRARE Pentru majoritatea procedeelor de conservare aplicate în industria conservelor vegetale,...
TURISM Originea termenului latină: turnare – a se întoarce turnus – mişcare circulară (călătorie cu întoarcere la punctul de rezidenţă)...
Te-ar putea interesa și
INTRODUCERE IN TEORIA GRAFURILOR Exista situatii când oameni ce lucreaza în diverse domenii ajung la reprezentarea unor cazuri concrete prin...
’’ Ideile, si daca sunt abstracte si daca nu, ca sa le poti manui, trebuie sa le ai. Calculatorul, ca sa-si faca treaba, trebuie sa inteleaga...
GRAFURI NEORIENTATE NOTIUNI INTRODUCTIVE NOTIUNI DE BAZA DEFINITIE: Se numeste graf neorientat o pereche ordonata de multimi(X,U), X fiind o...
Grafuri neorientate Definiţie. Se numeşte graf neorientat o pereche ordonată de mulţimi (X, U), X fiind o mulţime finită şi nevidă de elemente...
1. Introducere Numeroase situatii din viata cotidiana pot fi modelate cu ajutorul teoriei grafurilor. Teoria grafurilor este o importanta...
1. Preliminarii 1.1. Algoritmi Toti algoritmii descrisi în cadrul acestei lucrari folosesc structuri de date de tip graf. Unele descrieri sînt...
Capitolul 1 INTRODUCERE Pentru noţiunile din acest paragraf am consultat Behzad, Chartrand, Foster, Croitoru, Olaru, Tomescu. Alte completări...