Extras din curs
Codificare ¸si decodificare
1.1 Codificare
Definit¸ia 1.1 Fiind date mult¸imile A (alfabetul sursØa) ¸si B (alfabetul cod), o codificare
este o aplicat¸ie injectivØa K : A ! B¤.
Elementele mult¸imii K(A) µ B¤ se numesc cuvinte-cod, iar K(A) se nume¸ste cod.
DacØa B are numai douØa simboluri, codificarea K se nume¸ste binarØa.
Exemplul 1.1 Printre secvent¸ele binare de lungime 5, numØarul celor care au doi
de 1 este C2
5 = 10. Ele pot fi folosite pentru a codifica cifrele din scrierea zecimalØa
(Tabelul 1.1).
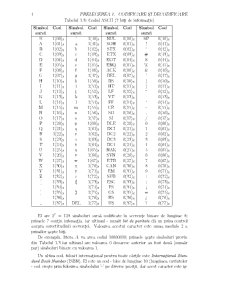
Tabelul 1.1: Codul ”doi-din-cinci”
Simbol zecimal Cuvˆant cod
1 11000
2 10100
3 01100
4 10010
5 01010
6 00110
7 10001
8 01001
9 00101
0 00011
Mesajul 0017300 are codul 110001000101100. De remarcat cØa ˆ1ntre cuvintele cod
nu se lasØa nici un spat¸iu, deoarece ”spat¸iu” poate fi el ˆ1nsusi un simbol-cod. Astfel
de exemplu, codul Morse are alfabetul B = f:;¡; spat¸iug.
Decodificarea se face foarte simplu: se ˆ1mparte mesajul codificat ˆ1n grupe de cˆate
cinci caractere ¸si se vede cifra din tabel corespunzØatoare grupei respective. Repartizarea
cuvintelor cod a fost fØacutØa pentru a realiza ¸si o decodificare pe baza unei
1
2 PRELEGEREA 1. CODIFICARE S¸I DECODIFICARE
formule. Astfel, dacØa a0a1a2a3a4 este cuvˆantul - cod, el corespunde cifrei k datØa de
algoritmul:
begin
x := a1 + 2a2 + 4a3 + 7a4;
if x = 11 then k := 0 else k := x;
end.
Definit¸ia 1.2 Pentru o codificare K : A ! B¤, se nume¸ste ”codificare a mesajelor
(textului) sursØa” aplicat¸ia K¤ : A¤ ! B¤ definitØa recursiv prin:
² K¤(²) = ² (² este cuvˆantul vid);
² K¤(a®) = K¤(a)K¤(®); 8a 2 A; ® 2 A¤.
Definit¸ia 1.3 Codificarea K este ”unic decodabilØa” dacØa K¤ este injectivØa.
Codificarea datØa ˆ1n Exemplul 1.1 este - dupØa cum s-a observat - unic decodabilØa.
Acest lucru nu este totdeauna posibil. DacØa luØam de exemplu codificarea
K(a) = 00; K(b) = 10; K(c) = 101; K(d) = 110; K(e) = 1001;
ea nu este unic decodabilØa; astfel K¤(bd) = K¤(cb) = 101110 .
Definit¸ia 1.4 1. O codificare K : A ! B¤ ˆ1n care toate cuvintele cod au lungimea
n se nume¸ste ”codificare-bloc de lungime n”, iar K(A) este un ”cod-bloc
de lungime n”.
2. O codificare K : A ! B¤ se nume¸ste ”instantanee” dacØa K(A) are proprietatea
prefixului (dacØa ®; ®¯ 2 K(B) atunci ¯ = ²).
Codul definit ˆ1n Exemplul 1.1 este un cod - bloc de lungime 5.
Codurile bloc sunt eficiente ˆ1n cazul cˆand simbolurile sursØa au frecvent¸e egale de
aparit¸ie; ˆ1n caz contrar, ele devin greoaie ¸si sunt preferabile codurile instantanee cu
lungimi variabile ale cuvintelor cod.
Preview document
Conținut arhivă zip
- Teoria Codurilor
- cod1.pdf
- cod10.pdf
- cod11.pdf
- cod12.pdf
- cod13.pdf
- cod14.pdf
- cod15.pdf
- cod16.pdf
- cod17.pdf
- cod18.pdf
- cod19.pdf
- cod2.pdf
- cod20.pdf
- cod3.pdf
- cod4.pdf
- cod5.pdf
- cod6.pdf
- cod7.pdf
- cod8.pdf
- cod9.pdf
Alții au mai descărcat și
ESTETICA “Ştiinţa care studiază legile şi categoriile artei, considerată ca forma cea mai înaltă de creare şi de receptare a frumosului; ansamblu...
Termenul de „arhivă” ce-l vom utiliza cu insistenţă pe parcursul cursului de faţă are o dublă semnificaţie. Pe de o parte, desemnează ansamblul de...
Conducerea preventivă reprezintă comportamentul rutier al participanţilor la trafic care asigură evitarea producerii unui accident, prin...
1.1. Introducere În medie peste 10000 de persoane au decedat anual din cauza cutremurelor de pamânt în secolul 20 (Bolt, 2001, vezi Figura 1.1)....
Tema 1: “Informaţii din balistica interioară şi exterioară.” Subiecte de studiu. 1. Informaţii despre balistica interioară. 2. Informaţii...
Relatiile, uneori conflictuale, dintre partenerii din diverse domenii si problemele complexe pe care organele judiciare le au de solutionat obliga...
Te-ar putea interesa și
INTRODUCERE Petrecând trei ani printr-o mulțime de informații juridice legate de toate acțiuniile și inacțiunile ființei umane și văzând că omul...
PRESCURTĂRI 1. INTRODUCERE O temă des cercetată în telefonia mobilă este eficienţa spectrală, care deobicei are înţelesul de densitatea...
Capitolul 1 Introducere in Sistemele de transmisiune a informației 1.1 - Despre informație Primele preocupări legate de informație au apărut,...
Introducere “Dacă vrei să cunoști principiile etice pe care le împartășește o companie, uităte la felul în care tratează oamenii: clienții,...
În domeniul matematicii și a ingineriei electronice, un cod Golay binar este un tip de cod de corectare liniară a erorilor utilizat în...
Pentru Saussure, simbolul este rezultatul uniunii semnificantului cu semnificatul, altfel spus, a formei expresiei şi a formei conţinutului. (Tran,...
Fragmentul debutează cu didascaliile care echivalează cu descrierea romanescă a spaţiului, timpului şi personajelor. Atât detaliile privind...
TUTORAT 1 UNIVERSUL SEMNULUI O INTRODUCERE Pentru a oferi noi repere societatii postmoderne a revolutiilor comunicarii si exploziei mediatice si...