Extras din curs
2.1 Reglarea automata a debitului
2.1.1 Estimarea paramatrilor proceselor de curgere
Pentru reglarea debitului se calculeaza modelul dinamic al unei conducte tehnologice prin care curge un
fluid, delimitata de elementul de executie si traductorul de debit. Un sistem de reglare automata a debitului SRA
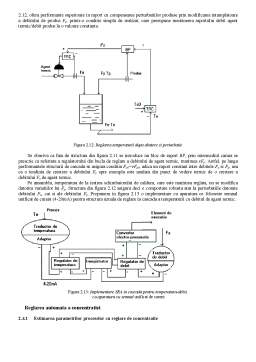
are reprezentarea conventionala din figura 2.1
Figura 2.1: Reprezentarea conventionala a unui SRA pentru debit
Unde:
F – debitul de fluid;
L – lungimea conductei;
D – diametrul conductei;
DP – caderea de presiune pe conducta;
F0 – valoerea presupusa a debitului;
Se presupune curgerea prin conducta a unui lichid incompresibil si se foloseste ecuatia de conservare a
impulsului, care actioneaza in sistem pentru doua cazuri distincte intalnite in practica:
a) conducte scurte cu L ~ D;
b) conducte lungi cu L >> D.
2.1.1.1 Modelul dinamic al unei conducte scurte
Se echivaleaza tronsonul de conducta cu o rezistenta hidraulica, pentru care este valabila relatia cunoscuta:
F a S 2 P
r
= D (2.1)
in care:
F este debitul care trece prin restrictie;
ΔP caderea de presiune pe restrictie;
a coeficientul de debit;
r densitatea fluidului.
Pentru regimul stationar de curgere se echilibreaza fortele care actioneaza in sistem si se obtine relatia:
2
0
0 2 2 0
2
P S F S
S
r
a
D - = (2.2)
in care:
0 DP S este forta activa de apasare asupra lichidului din conducta;
2
0
2 2 2
F S
S
r
a
forta de reactiune datorata restrictiei.
In regim dinamic diferenta dintre cele doua forte este compensata de viteza de variatie in timp a impulsului din
sistem:
2
2 2
( ) ( ) ( )
2
P t S F t S d Mv
S dt
r
a
D - = (2.3)
In (2.3) M este masa de lichid din conducta, iar n este viteza sa de deplasare (curgere).
Atunci pentru exprimarea din (2.3) avem:
2
2 2
( ) ( ) 1 ( ( ))
2
P t S F t S LS d F t
S S dt
r r
a
D - = (2.4)
Marimile care depind de timpul t in (2.4) se obtin daca se dau variatii arbitrare peste valorile de regim
stationar, astfel:
0 0
0
( ) ( ( )) ( )
( ) ( )
P t P P t P p t
F t F F t
D = D + D D = D + D
= + D
(2.5)
Din (2.4) si (2.5) se obtine:
( ( ) ) ( ( ) ) ( ( ) )
2
0
0 2 2 2 0
F F t d P p t S S L F F t
S dt
r
r
a
+ D
D + D - = + D (2.6)
Daca se extrage din (2.6), regimul stationar exprimat prin (2.2), si se neglijeaza termenul patratic DF2 ( t ) se
obtine:
0 ( ) ( ( ) )
2 2
2
( )
2
F F t d p t S S L F t
S dt
r
r
a
D
D - = D (2.7)
Prin normare la valorile de regim stationar avem:
( ) ( )
( ) ( )
0
0
F t
y t
P
p t
m t
P
D
=
D
=
D
Rezulta modelul liniarizat cu variabile adimensionale:
2 0 ( ) ( ) ( )
0
1
2
V dy t y t m t
F dt
a + = (2.8)
unde cu V0 s-a notat volumul de fluid din conducta, ocupat in regim stationar.
Din ecuatia diferentiala (2.8), prin aplicarea transformatei Laplace, se obtine usor functia de transfer a
canalului de executie:
( ) 1
p
pa
pa
k
H s
t s
=
+ (2.9)
unde kp este factorul de amplificare, iar pa t constanta de intarziere a canalului considerat, 0.5 p k = si
2 0
0
pa
V
F
t = c .
Pentru un fluid compresibil, calculul este similar, cu cel anterior cu diferenta ca ecuatia (2.1) este corectata
cu un coeficient de compresibilitate.
Preview document
Conținut arhivă zip
- Curs SCPI.pdf