Estimare și Identificare - Introducere

INTRODUCERE

1.1 PROCESE

1.1.1 Definiţia unui proces

Cea mai simplă definiţie a unui proces este aceea a unui sistem fizic care

evoluează în timp sub efectul diverselor influenţe interne şi externe. De regulă, asupra unui proces acţionează mărimi de intrare, mărimi de ieşire şi perturbaţii (fig. 1.1).

Fig. 1.1 Explicativă privind definirea unui proces.

Se poate spune că un proces este traversat de un flux de materie, energie şi informaţie. Mărimile de ieşire sunt variabile măsurabile, sau mai puţin perceptibile, caracterizând evoluţia procesului. Mărimile de intrare sunt variabile de origine externă susceptibile de-a influenţa evoluţia procesului. Atunci când se poate acţiona asupra variabilelor de intrare aceste mărimi poartă denumirea de variabile de comandă. Independent de mărimile de intrare şi ieşire, este posibil de-a constata existenţa unor alte variabile caracteristice procesului a căror evoluţie este susceptibilă de-a influenţa mărimile de ieşire. În general un proces este descris printr-un model, ansamblu de relaţii de natură matematică, care permit o estimarea satisfăcătoare a evoluţiei variabilelor sistemului care interesează utilizatorul. Este evident faptul că un model constituie o abstractizare având ca obiectiv obţinerea unei descrieri simple a realităţii, procesul existând independent de toate modelele.

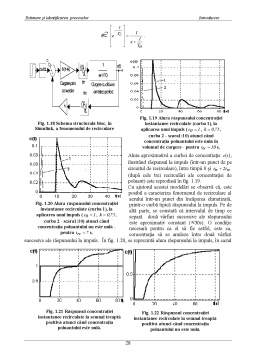
Exemplul 1.1 Modelarea procesului de recirculare a aerului într-o încăpere. Recircularea aerului în interiorul unei încăperi este efectul introducerii unui aer proaspăt la intrarea în încăpere, peste un aer care este neîmprospătat din cauza degajărilor termice sau celor de nocivităţi, ceea ce contribuie la creşterea calităţii aerului în zonele ocupate de personal. Se consideră o încăpere în care se degajă o anumită cantitate de poluant, în ipoteza că această degajare este constantă în timp, ca şi concentraţia aceleiaşi nocivităţi în aerul introdus, iar ventilarea este uniformă în întreg spaţiul incintei şi nu există alte degajări (de temperatură sau umiditate), ecuaţia diferenţială de bilanţ masic este

, (1.1)

în care: este debitul volumic de aer refulat, respectiv evacuat în şi din incintă, în m3.s-1; este debitul masic de poluant (substanţă nocivă) degajat în incintă, în kg.s-1; este concentraţia poluantului în aerul refulat, în kg.m-3; este concentraţia poluantului în aerul din încăpere, variabilă în timp, în kg.m-3; este timpul, în s; este volumul încăperi, în m3.

Ecuaţia (1.1) poate fi scrisă sub forma [36]:

.

Integrând ecuaţia, se obţine succesiv

, (1.2)

unde: c0 este valoarea concentraţiei poluantului în aerul din incintă, la timpul t=0, iar c este valoarea concentraţiei, la timpul t. Notând rapoartele , (ds, debitul specific de substanţă nocivă degajată), relaţia (1.2) devine

. (1.3)

Din ecuaţia (1.3) rezultă concentraţia finală a poluantului în aerul din încăpere

. (1.4)

În cazul în care aerul refulat nu conţine substanţa respectivă (cr=0), atunci

, (1.5)

iar dacă iniţial, în încăpere nu există substanţă nocivă (c0=0)

. (1.6)

Atunci când în încăpere nu există substanţă nocivă (c0=0), şi când aerul refulat nu conţine substanţa respectivă relaţia (1.4) devine

. (1.7)

Dacă se ţine cont că, debitul masic al poluantului este produsul dintre debitul volumic D1 şi concentraţia poluantului c1 (D1m=c1D1), atunci relaţia (1.7) devine

, (1.8)

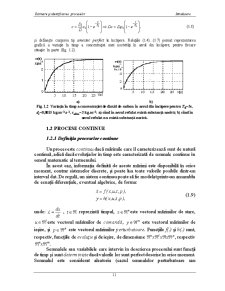
şi defineşte curgerea tip amestec perfect în încăpere. Relaţiile (1.4)...(1.7) permit reprezentarea grafică a variaţie în timp a concentraţiei unei nocivităţi în aerul din încăpere, pentru fiecare situaţie în parte (fig. 1.2).

a) b)

Fig. 1.2 Variaţia în timp a concentraţiei de dioxid de carbon în aerul din încăpere pentru T0=5s, ds=0,0015 kg.m-3.s-1, cadm=3 kg.m-3: a) când în aerul refulat există substanţă nocivă; b) când în aerul refulat nu există substanţă nocivă.

1.2 PROCESE CONTINUE

1.2.1 Definiţia proceselor continue

Un proces este continuu dacă mărimile care îl caracterizează sunt de natură

continuă, adică dacă evoluţia lor în timp este caracterizată de semnale continue în sensul matematic al termenului.

În acest caz, informaţia definită de aceste mărimi este disponibilă în orice moment, contrar sistemelor discrete, şi poate lua toate valorile posibile dintr-un interval dat. De regulă, un sistem continuu poate să fie modelat printr-un ansamblu de ecuaţii diferenţiale, eventual algebrice, de forma: