Modelarea Ball & Beam Experiment

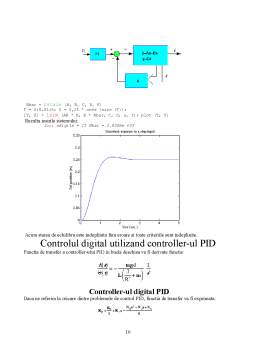
O minge este plasat pe o grindă, a se vedea figura de mai jos, în cazul în care este permis să se rostogoleasca cu 1 grad de libertate de-a lungul grindei. Un braţ de pârghie este anexat la grinda la un capăt şi o roata de andrenaj la celalat capat. Alpha este unghiul de inclinare a grindei si theta este unghiul de rotatie al parghiei. Cand unghiul este schimbat de la poziţia verticală, din cauza gravitatii mingea incepe sa se rostogoleasca de-a lungul grindei. Va fi proiectat un controller pentru acest sistem, astfel incat pozitia mingii sa poata fi manipulata.

Pentru această problemă, vom presupune că mingea se rostogoleste, fără alunecare şi frecarea între grindă şi minge este neglijabilă. Se dau urmatoarele valori:

M masa minge

0,11 kg

R rază minge

0,015 m

d pârghie braţ offset

0,03 m

g acceleraţie gravitaţională

9,8 m / s ^ 2

L lungimea grindei

1,0 m

J momentul de inertie al bilei

9.99e-6 kgm ^ 2

r pozitia mingei pe grinda

alfa

unghiul inclinatie grinda

theta unghi rotatie

Criterii pentru această problemă sunt:

- Stabilirea de timp mai mic de 3 secunde

- Depăşiri mai mici de 5%

Sistemul de ecuatii

Ecuaţia de mişcare a mingii este data de:

Prin liniarizarea ecuatiei, cand alpha=0 este:

Ecuatia unghiului de rotatie va fi:

Înlocuind în ecuaţia anterioara, ajungem:

Funcţia de transfer

Transformata Laplace a ecuatie de mai sus este:

Rezulta ca functia de transfer a pozitie mingii R(s) in functie de unghiul theta, este:

Trebuie remarcat faptul că funcţia de transfer de mai sus este un integrator de dublu. Astfel, are o marjă mică de stabilitate şi va oferi o problemă dificilă de control.

State-Space

Sistemul liniar de ecuaţii poate fi, de asemenea, reprezentat în formă State-Space. Aceasta se poate face prin selectarea poziţiei mingea (r) şi viteza (rdot), ca variabile de stare şi unghiul (theta) ca subsistem de intrare.