Extras din curs
SINTEZA CLASICĂ
A
SLC
Capitolul 10
2
Tematică
- Etapele sintezei clasice a SLC
- Minimizarea func țiilor de comutație
folosind diagramele KV
- Minimizarea funcțiilor de comutație
folosind diagramele VEM
- Sinteza cu ajutorul multiplexoarelor şi
decodificatoarelor
3
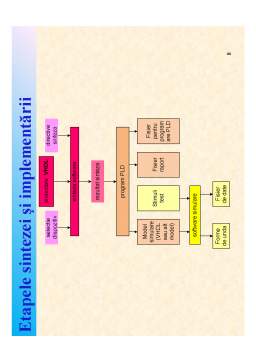
Etapele sintezei clasice a SLC
E1. Pornind de la descrierea verbală (neformalizată) a func țiilor realizate de
schema sintetizată, se generează schema bloc a acesteia. Schema bloc permite crearea
unei imagini mai clare asupra schemei sintetizate punând în evidență toate comenzile
externe și ieșirile din schemă. Fiecare semnal are un nume (mnemonic) care să
sugereze cât mai clar semnificația semnalului. Pentru toate semnalele se va preciza
grafic și prin convenții legate de nume logica de activare a semnalului.
E2. Se descriu printr-una dintre metodele cunoscute (vezi capitolele 3 și 4)
funcțiile aferente semnalelor de ieșire. Tabelele de adevăr sunt utilizate doar pentru
funcții dependente de un număr mic de variabile (cel mult 4-5 variabile). Pentru
funcții cu un număr mai mare de variabile se pot utiliza reprezentări simbolice
disjunctive sau conjunctive dar în unele situații funcțiile se reprezintă direct prin
forme logice necanonice.
E3. Se alege metoda de implementare.
E4. În funcție de metoda de implementare aleasă vor fi prelucrate funcțiile deduse
în etapa E2 cu scopul de a obține o implementare cu complexitate cât mai mică.
E5. Se analizează schema în ipoteza lipsei întârzierilor, cu scopul de a verifica dacă
sinteza a fost realizată corect.
4
Etapele sintezei clasice a SLC
E6. Se aleg din catalog componentele concrete pentru implementare.
E7. Se editează schema i se testează func ionarea ei în condi ii ș ț ț cât mai apropiate
de cele ale funcționării reale. Simularea permite punerea în evidență a unor anomalii
datorate întârzierilor în propagarea semnalelor. Dacă anomaliile semnalate se
consideră periculoase și nu pot fi eliminate prin măsuri directe (de exemplu
echilibrarea schemei), se poate relua sinteza de la etapa E6 sau chiar de la etapa E3.
E8. Se realizează documentația aferentă schemei sintetizate și se trece la
implementarea prototipului. Dacă testele efectuate pe prototip nu pun în evidență
nici o anomalie, se poate trece la producția de serie. Dacă apar anomalii ce nu au
putut fi dedectate prin simulare, se reia sinteza fie alegând alte componente pentru
implementare fie alegând o altă metodă de sinteză.
5
Pre ul de cost al ț unei forme logice
Evaluarea prețului de cost al unei porți logice se bazează pe ipoteza că acesta este
direct proporțional cu numărul de intrări ale porții logice adică:
PCp=k·i
unde
i – numărul de intrări în poarta logică;
k – prețul pe o intrare a porții logice.
Acceptând pentru simplitate că toate porțile logice au același preț de cost mediu pe
intrare, prețul de cost al unei scheme S realizată cu porți logice poate fi calculat cu
relația:
PC(S) =
unde
i - numărul de intrări pe o poartă;
ni – numărul porților cu i intrări.
6
Acoperire minimă
Vom numi acoperire minimă o formă booleană cu preț de cost
minim atașată unei funcții de comutație date.
Exemplu: Se consideră funcția f(x,y,z) = S(0,1,5,7)
După cum se știe, această funcție poate fi reprezentată prin forma canonică normal
disjunctivă:
Prețul de cost al acestei forme este PC1(f) = 3·1+4·3+1·4 = 19
Aplicând axiomele și teoremele algebrei booleene asupra formei canonice de mai
sus, rezultă
Se observă că pentru această formă PC2(f*) = 2·1+3·2 = 8.
Deoarece ultima formă obținută nu mai poate fi redusă, rezultă că PC2 este valoarea
minimă pentru formele minime disjunctive atașate funcției f deci f* este acoperire
minimă pentru funcția dată.
Preview document
Conținut arhivă zip
- PSD01.pdf
- PSD02.pdf
- PSD03.pdf
- PSD04.pdf
- PSD05.pdf
- PSD06.pdf