Cuprins
- CAPITOLUL 1 INTRODUCERE 9
- 1.1Scurt istoric 9
- 1.2Definiţii 12
- 1.3Structuri de sisteme de reglare automată 19
- 1.4Clasificarea sistemelor automate 22
- 1.5Problematica automatizării proceselor 24
- CAPITOLUL 2 MODELE MATEMATICE 25
- 2.1Noţiuni introductive 25
- 2.2Modele intrare - ieşire 26
- 2.2.1Ecuaţii diferenţiale 26
- 2.2.2Funcţia de transfer 29
- 2.2.2.1Definire 29
- 2.2.2.2Funcţiile de transfer ale conexiunilor de elemente 31
- 2.2.2.3Simplificarea (reducerea) schemelor bloc 36
- 2.2.3Tipuri de elemente funcţionale 39
- 2.3Modele de tipul intrare-stare-ieşire 40
- 2.3.1Definire 40
- 2.3.2Relaţia dintre modelul intrare-stare-ieşire şi funcţia de transfer 47
- 2.3.3Realizări. Echivalenţe 49
- 2.3.3.1Realizări 49
- 2.3.3.2Echivalenţe 54
- 2.3.4Discretizarea sistemelor netede 55
- 2.3.4.1Noţiuni introductive 55
- 2.3.4.2Eşantionarea semnalelor 55
- 2.3.4.3Discretizarea semnalelor 57
- 2.3.5Proprietăţile structurale ale sistemelor liniare 60
- 2.3.5.1Controlabilitatea 60
- 2.3.5.2Observabilitatea 63
- 2.4Sisteme cu parametri distribuiţi şi cu timp mort 65
- 2.4.1Sisteme cu parametri distribuiţi 65
- 2.4.2Sisteme cu timp mort 66
- 2.4.2.1Sisteme netede cu timp mort 66
- 2.4.2.2Sisteme discrete cu timp mort 67
- CAPITOLUL 3 ANALIZA SISTEMELOR LINIARE DE REGLARE AUTOMATĂ 69
- 3.1Introducere 69
- 3.2Caracteristici de timp 71
- 3.2.1Introducere 71
- 3.2.2Funcţia pondere 73
- 3.2.3Funcţia indicială 76
- 3.3Caracteristici de frecvenţă 77
- 3.3.1Introducere 77
- 3.3.2Locul de transfer (Nyquist) 78
- 3.3.3Caracteristici logaritmice de frecvenţă (Bode) 84
- 3.4Analiza calităţii sistemelor de reglare automată netede invariante 94
- 3.4.1Generalităţi 94
- 3.4.2Stabilitatea 94
- 3.4.2.1Introducere 94
- 3.4.2.2Criteriul de stabilitate Routh-Hurwitz 98
- 3.4.2.3Criteriul de stabilitate Nyquist101
- 3.4.2.4Criteriul de stabilitate practic al lui Bode104
- 3.4.3Analiza regimurilor tranzitorii106
- 3.4.3.1Analiza prin metode de timp106
- 3.4.3.2Analiza prin metode de frecvenţă111
- 3.4.4Analiza regimului staţionar115
- 3.4.4.1Erori în regim permanent (staţionar)115
- 3.4.4.2Indicii de calitate ai regimului permanent (staţionar)118
- 3.4.4.3Influenţa perturbaţiei asupra erorii119
- 3.5Analiza sistemelor discrete de reglare automată120
- 3.5.1Calculul răspunsului120
- 3.5.2Stabilitatea sistemelor discrete123
- 3.5.3Calculul erorii în regim staţionar125
- 3.5.4Refacerea semnalului126
- 3.6Analiza SRA prin metoda locului rădăcinilor128
- 3.6.1Definirea şi construcţia locului rădăcinilor128
- 3.6.2Utilizarea LR în analiza SRA131
- CAPITOLUL 4 SINTEZA SISTEMELOR CONVENŢIONALE DE REGLARE AUTOMATĂ133
- 4.1Noţiuni introductive133
- 4.2Problematica generală a proiectării regulatorului134
- 4.3Proiectarea regulatorului pentru sisteme monovariabile141
- 4.3.1Formularea problemei de proiectare141
- 4.3.2Clasificarea compensatoarelor144
- 4.3.3Sinteza compensatorului serie în c.c. pentru sistemele netede145
- 4.3.3.1Metoda alocării polilor şi zerourilor146
- 4.3.3.2Metoda caracteristicilor logaritmice de frecvenţă148
- 4.3.3.3Metoda caracteristicilor amplitudine-fază149
- 4.3.4Sinteza compensatorului serie pentru sistemele discrete152
- 4.3.4.1Sinteza sistemelor discrete pe baza funcţiilor de transfer152
- 4.3.4.2Sinteza algoritmilor numerici prin metode de frecvenţă155
- 4.4Alegerea regulatorului156
- CAPITOLUL 5 SENSIBILITATEA SISTEMELOR160
- 5.1Definirea şi importanţa sensibilităţii160
- 5.2Metode de calcul161
- 5.2.1Metode analitice161
- 5.2.2Metode experimentale166
- 5.3Sensibilitatea sistemelor167
- 5.3.1Sensibilitatea funcţiei de transfer167
- 5.3.2Sensibilitatea parametrilor de calitate ai reglării171
- 5.3.3Sensibilitatea parametrilor de structură ai sistemului175
- CAPITOLUL 6 SISTEME ROBUSTE178
- 6.1Incertitudinile sistemelor178
- 6.1.1Incertitudini structurate178
- 6.1.2Incertitudini nestructurate181
- 6.1.3Metode de conducere a sistemelor cu incertitudini182
- 6.2Determinarea limitelor de variaţie ale incertitudinilor183
- 6.2.1Introducere183
- 6.2.2Proiectarea stabilităţii robuste184
- 6.3Stabilizarea robustă187
- 6.3.1Condiţii de stabilitate robustă187
- 6.3.2Modelul generalizat192
- 6.3.3Soluţia problemei sintezei robuste198
- Anexa 1203
- Anexa 2207
- Bibliografie211
Extras din curs
În evoluţia sa omenirea a fost preocupată de realizarea unor dispozitive, mijloace tehnice, care să solicite cât mai puţin prezenţa omului pentru o funcţionare corespunzătoare sau să funcţioneze fără intervenţia omului.
Cel mai vechi dispozitiv cu reacţie cunoscut se pare că este ceasul cu apă al lui Ktesibios din Alexandria (contemporan cu Aristachos, Euclid, Arhimede, regele Ptolemeu II Philadelphus (285-247 î.e.n.)).
Variabila reglată din proces este nivelul apei din vasul regulator. Acesta este reglat de un flotor care deschide orificiul de alimentare atunci când nivelul apei scade şi îl închide când creşte. În acest mod debitul apei care ajunge din vasul regulator în recipient este menţinut constant. În recipient se află un plutitor pe care este prinsă o figurină care se ridică o dată cu creşterea nivelului lichidului şi indică timpul scurs.
Ceasul cu apă a pătruns şi în Orientul Mijlociu, utilizarea sa menţinându-se până la invazia mongolilor în Bagdad în anul 1258.
Un alt dispozitiv antic care utilizează conceptul reacţiei pentru reglarea nivelului unui lichid este lampa cu petrol a lui Philon.
Interesul pentru utilizarea reacţiei pentru realizarea unor obiective se regăseşte în Europa începând cu secolul al XVI-lea când Cornelis Drebbel
(1572-1633) inventează regulatorul de temperatură utilizat într-un incubator de pui.
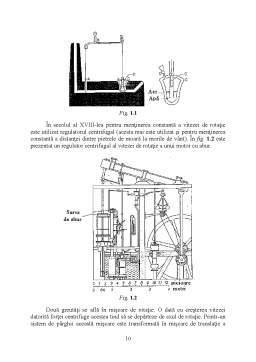
În America William Henry (1729-1786) inventează regulatorul de temperatură din fig. 1.1. Sesizorul de temperatură D comandă debitul de agent termic A. Aerul din vasul C se dilată o dată cu creşterea temperaturii şi prin presiunea exercitată asupra nivelului apei din vas determină ridicarea nivelului acesteia în tubul vertical. Prin intermediul plutitorului D, cu ajutorul unui sistem de pârghii, mişcarea se transmite la supapa de reglare a debitului de agent termic A.
Fig. 1.1
În secolul al XVIII-lea pentru menţinerea constantă a vitezei de rotaţie este utilizat regulatorul centrifugal (acesta mai este utilizat şi pentru menţinerea constantă a distanţei dintre pietrele de moară la morile de vânt). În fig. 1.2 este prezentat un regulator centrifugal al vitezei de rotaţie a unui motor cu abur.
Fig. 1.2
Două greutăţi se află în mişcare de rotaţie. O dată cu creşterea vitezei datorită forţei centrifuge acestea tind să se depărteze de axul de rotaţie. Printr-un sistem de pârghii această mişcare este transformată în mişcare de translaţie a supapei de admisie a aburului care va micşora debitul de abur şi o dată cu aceasta viteza de rotaţie a motorului. La scăderea vitezei de rotaţie a motorului apropierea greutăţilor de axul de rotaţie va avea ca efect mărirea debitului de abur care va conduce la o mărire a vitezei motorului. În acest mod viteza de rotaţie este menţinută la valoarea constantă dorită.
Dezvoltarea şi îmbunătăţirea regulatorului centrifugal a mărit interesul pentru analiza comportării dinamice a acestuia. În anul 1807 în volumul I al cărţii „Lectures on Natural Philosophy and the Mechanic Arts” Thomas Young dă o formulă pentru masele greutăţilor sferice. Jean-Victor Poncelet publică în „Cours de Mecanique” în anul 1826 ecuaţiile de echilibru ale regulatorului. William Thomson şi James Clerk Maxwell se preocupă cu modelarea regulatorului şi problema instabilităţii sistemelor dinamice. În 1868 Maxwell determină condiţiile de stabilitate pentru un sistem de ordinul trei utilizând metoda ecuaţiilor diferenţiale liniare. În anul 1874 Edward John Routh a prezentat un criteriu de stabilitate pentru sistemele de ordinul cinci, iar în 1876 o generalizare cunoscută acum sub numele de „criteriul de stabilitate Routh”. În anul 1895 matematicianul Adolf Hurwitz prezintă un alt criteriu de stabilitate cunoscut sub numele de „criteriul de stabilitate Hurwitz”. Bompiani demonstrează în 1911 că cele două criterii de stabilitate, Routh şi Hurwitz, sunt echivalente.
Utilizarea energiei electrice a ridicat probleme noi de reglare automată (reglarea distanţei dintre electrozi la lămpile cu arc electric, reglarea frecvenţei, vitezei motoarelor electrice, poziţiei etc.) care se multiplică cu apariţia electronicii. Totodată se dezvoltă noi metode de studiu a unor dispozitive electronice care se pot aplica însă în general tuturor sistemelor automate: metoda răspunsului în frecvenţă datorată lui Harry Nyquist (1889-1976), metode de proiectare logaritmice de fecvenţă datorate lui Hendrik W. Bode.
Al doilea război mondial impune cerinţe de realizare a unor sisteme automate de înaltă performanţă. Ca urmare, are loc o unificare a teoriilor care au o mare gamă de aplicabilitate în domenii diverse de activitate (chimic, electric, mecanic, naval, aeronautică etc.).
De asemenea, sistemele de comandă numerice apar tot în cursul acestei perioade. Apariţia sistemelor radar implică un nou tip de sisteme automate - sistemele cu eşantionare, care la rândul lor necesită o teorie adecvată pentru studiu şi analiză (teoria transformatei Z).
În teoria sistemelor automate domină metodele de frecvenţă până în
anii ’50. În 1948 apare metoda locului rădăcinilor datorată lui Evans. De asemenea, în perioada anilor 50 începe să fie utilizat şi conceptul de „spaţiu al stărilor”, deşi vechimea sa este mult mai mare (1844).
Dezvoltarea informaticii şi electronicii conduce la crearea unor procese şi produse noi în care un rol important îl au sistemele de reglare automată. Majoritatea acestor produse au drept scop mărirea productivităţii şi înlocuirea activităţii umane cu cea a unor maşini. Pe această linie se înscrie şi utilizarea liniilor de producţie robotizate într-o măsură din ce în ce mai mare.
1.2Definiţii
Proces fizic. Prin proces fizic se înţelege tranziţia unui „sistem termodinamic” dintr-o „stare termodinamică” în alta, tranziţie ce se evidenţiază într-o accepţiune tehnologică prin transferuri energetice şi masice.
Sistem termodinamic. Prin sistem (fizic) termodinamic se înţelege orice porţiune din univers pentru care se poate delimita un „interior” şi un „exterior”, interiorul conţinând un număr oarecare de corpuri macroscopice considerate ca având o structură (fizică) continuă.
Bibliografie
BARN69BARNETT, S. - Insensitivity of control systems. În Int. J. Control, 1969, Vol. 10, nr. 6, pp. 665675
BICĂ94aBICĂ, M. - Produse program utilizate în analiza şi sinteza sistemelor, Referat de doctorat, Academia Tehnică Militară, Bucureşti, 1994
BICĂ94bBICĂ, M. - Robusteţea şi senzitivitatea sistemelor automate, Referat de doctorat, Academia Tehnică Militară, Bucureşti, 1994
BICĂ95aBICĂ, M. - Metoda senzitivităţii (sensibilităţii) utilizată în studiul fiabilităţii parametrice a sistemelor automate, A XXVI-a Sesiune de comunicări ştiinţifice cu participare internaţională a Academiei Tehnice Militare, Vol. 5, pag. 9299, Bucureşti, 1995
BICĂ95bBICĂ, M., CIUPITU, C. - Îndrumar pentru proiectarea sistemelor automate liniare netede, Editura Academiei Tehnice Militare, Bucureşti, 1995
BICĂ96BICĂ, M., ŞERB, A. - Unele aspecte privind sensibilitatea sistemelor automate, Întâia Sesiune de comunicări ştiinţifice a Academiei Trupelor de Uscat „Nicolae Bălcescu” Sibiu, 1996
BICĂ99BICĂ, M. - Fiabilitatea parametrică a sistemelor automate, Teză de doctorat, Bucureşti, 1999, Academia Tehnică Militară
BICĂ00BICĂ, M. - The uncertainties of linear control systems modelling, International Conference AUTOMATICS AND INFORMATICS '2000, Sofia, Bulgaria, 2000
BODE45BODE, H. W. - Network analysis and feedback amplifiers design, Princeton, New York, van Nostrad, 1945
CHAN72CHANG, S. S. L., PENG, T. K. - Adaptive guaranteed cost control of systems with uncertain parameters, IEEE Transactions on Automatic Control, AC-17 (August, 1972), pp. 474483
CIUP78CIUPITU, C. - Automatica şi calculatoare analogice, Vol. 1. Modele matematice ale sistemelor şi modelarea lor pe calculatoare electronice, Editura Academiei Militare, Bucureşti, 1978
DEME74DEMETER, Ş. - Îndrumar pentru proiectarea sistemelor de urmărire automată, Academia Militară, Bucureşti, 1974
DUMI85DUMITRACHE, I., CĂLIN, S., BOŢAN, C., NIŢU, C. - Automatizări electrice şi electronice, Editura Didactică şi Pedagogică, Bucureşti, 1985
DUMI93DUMITRACHE, I, DUMITRU, S., MIHU, I., MUNTEANU, F., MUSCĂ, GH., CALCEV, C. - Automatizări electronice, Editura Didactică şi Pedagogică, Bucureşti, 1993
DUMI99DUMITRACHE, I, MIHU, I. - Robusteţea sistemelor de reglare cu predictor Smith, Seminar: teorii de tip Popov prezent şi actualitate, Academia Română, Bucureşti, 25 noiembrie 1999
ESLA80ESLAMI, M., RUSSELL, D. L. - On stability with large parameter variations stemming from the direct method of Lyapunov, IEEE Transactions on Automatic Control, AC-25,6 (december, 1980), pp. 12311234
HAVE95HAVERKORT, B. R., MEEUWISSEN, M., H., A. - Sensitivity and Uncertainty Analysis of Markov-Reward Models, IEEE Transactions on Reliability, Vol. 44, no. 1, 1995, march
HAWA84EI-HAWARY, M. E. - Control System Engineering, 1984 by Reston Publishing Company, Inc., A Prentice-Hall Company
HINR86HINRICHSEN, D., PRITCHARD, A. J. - Stability radius of linear systems, Systems and Control Letters, 7 (1986), pp. 110
HORO68HOROWITZ, I. M. - Design of zero sensitivity, Int. Symp. On Network Theory, ETAN Belgrad, september, 1968
HORR76HORRISBERGER, H. P., BELANGER, P. R. - Regulators for linear time invariant plants with uncertain parameters, IEEE Transactions on Automatic Control, AC-21, 5 (october, 1976),
pp. 705708
Preview document
Conținut arhivă zip
- ANEXA1.DOC
- ANEXA2.DOC
- BIBLIOGRAFIE.DOC
- CAP1.DOC
- CAP2-1.DOC
- CAP2-2.DOC
- CAP3-1.DOC
- CAP3-2.DOC
- CAP3-3.DOC
- CAP4-1.DOC
- CAP4-2.DOC
- CAP5.DOC
- CAP6.DOC
- CUPRINS.DOC
- PREFATA.DOC