Extras din curs
Din m feluri de materii prime M_(i ) (i∈[1,m]), disponibile in cantitati b_(i ) (i∈[1,m]), se preconizeaza a se realiza n tipuri de produse P_(j ) (j∈[1,n]), care necesita consumurile specifice a_(ij ) (i∈[1,m],j∈[1,n]). Beneficiul obtinut pentru fiecare unitate de produs este c_(j ) (j∈[1,n]). Sa se determine ce cantitate trebuie sa se fabrice din fiecare produs astfel incat beneficiul total sa fie maxim.
Daca se noteaza necunoscutele (variabilele) cu x_j ,j∈[1,n], atunci
z=∑_(j=1)^n▒〖c_j x_j 〗
reprezinta expresia beneficiului total care trebuie sa fie maxim. Conditia (restrictia):
a_i1 x_1+a_i2 x_2+⋯+a_in x_n≤b_i
se impune pentru ca materia prima M_(i )este disponibila in cantitatea limitata b_(i )si tot ceea ce se consuma pentru fabricarea cantitatilor x_j de produse P_(j )nu poate sa depaseasca disponibilul. In functie de semnificatia practica a variabilelor se stabileste si semnul acestora.
Daca in locul beneficiilor unitae se cunosc costurile unitare, atunci z reprezinta costul total care trebuie sa fie minim.
Coeficientii a_(ij ) (i∈[1,m],j∈[1,n]) se numesc consumuri specifice sau coeficienti tehnologici.
Daca se noteaza c=〖(c_1 c_2 c_n)〗^T, b=〖(b_1 b_2 b_m)〗^T, x=〖(x_1 x_2 x_n)〗^T, 〖A(a_ij)〗_█(i=1,m@j=1,n) atunci modelul matematic al problemei se scrie vectorial astfel:
{█(maxim f(x_1 x_2 x_n )=∑_(j=1)^n▒〖c_j x_j 〗@Ax≤b@x≥0)┤
Cunoasterea marimilor x_j reprezinta scopul final intr-o problema de planificare a productiei.
In aceste conditii, din resursa totala s-u consumat in total cantitatea ∑_(j=1)^n▒〖a_ij x_j 〗, costul total al materiei prime consumate este α_i ∑_(j=1)^n▒〖a_ij x_j 〗.
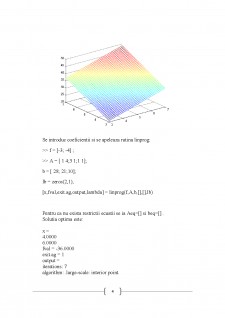
Rezolvarea unei probleme de acest tip se poate face prin utilizarea rutinei linprog continuta in Optimization Toolbox al lui Matlab.
Fie sistemul:
{█((max(3x_1+4x_2))¦(x_1+4x_2≤28)@(3x_1+x_2≤21)¦(x_1+x_2≤10)@(x_1≥0)¦(x_2≥0))┤
unde f, x, b, beq, lb si ub sunt vectori si A si Aeq sunt matrici.
Sintaxa este:
[x, fval, exitflag, output, lambda] = linprog(f, A, b, Aeq, beq, lb, ub, x0, options)
Preview document
Conținut arhivă zip
- Algoritmi genetici.docx
Alții au mai descărcat și
C1.1.CONCEPTUL DE CAD TERMINOLOGIE - COMPUTER AIDED ENGINEERING -CAE-vizeazăetapeledecercetare,inovaresiconcepţie; - COMPUTER AIDED DRAWING/...
Răspunsuri Arbori şi păduri 1. D. O relaţie de încredere oferă posibilitatea folosirii în comun doar a resurselor între domenii; ea nu oferă în...
Lecţia 1 Introducere în securitatea informaţională 1.Informaţia ca obiect de valoare şi protecţie 4 2.Conceptele de bază ale Securităţii...
Introducere I. Documente electronice – definire, caracteristici şi tipologie I. 1. Delimitări terminologice I. 2. Document text I. 3....
Capitolul 1.BAZE METODOLOGICE ALE EVALURII EFICIENŢEI INVESTIŢIILOR ÎN IT&C 1.1. Evaluarea eficienţei în condiţiile specifice investiţiilor din...
. Notiuni introductive Un sistem de calcul poate contine sute sau mii de componente individuale (circuite integrate, diode, rezistoare,...
I. SISTEME INFORMATICE I. 1. NOTIUNEA DE “SISTEM” În general, un sistem se defineste ca fiind un ansamblu de elemente fizice si logice...
Concepte de bază Un sistem de baze de date: este un sistem computerizat de păstrare a înregistrărilor al cărui scop principal este să stocheze...
Te-ar putea interesa și
1. Algoritmi Genetici 1.1. Introducere În ultimii ani, metodele bazate pe algoritmi genetici s-au bucurat de succes în domeniul cercetărilor...
Conceptul de evoluţie a fost propus de savantul englez Charles Darwin în 1859 în celebra sa carte “Originea speciilor prin selecţie naturală”....
1. REZUMAT Un algoritm genetic efectuează operaţii specifice în cadrul unui proces de reproducere guvernat de operatori genetici. Noile soluţii...
Algoritmi genetici Tehnici adaptive de cautare euristica, bazate pe principiile geneticii si ale selectiei naturale Lucreaza cu o populatie de...
1. Rezumat Algoritmii genetici sunt tehnici adaptive de căutare euristică, bazate pe principiile geneticii şi ale selecţiei naturale, enunţate de...
1 Istoric Inceputurile algoritmilor geneticise situeaza undeva in jurul anului 1950, cand mai multi biologi au folosit calculatoarele pentru...
1 Introducere în calculul evolutiv În general, orice sarcina abstracta care trebuie îndeplinita, poate fi privita ca fiind rezolvarea unei...
Calculul cognitiv denotă o familie de metode de rezolvare a problemelor care imită inteligenţa “găsită” în natură. Obiectivul comun al acestor...