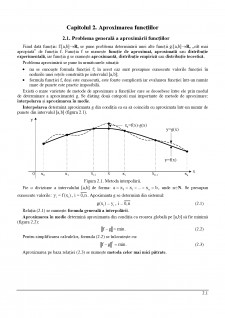
Extras din curs
Fie a ?R =i a* ?R un num[r ,,apropiat" de a. Num[rul a se nume=te valoare exact[ iar a* ?R ,
aproximaie a lui a. }n aceast[ situaie vom nota: a ? a*
Se nume=te eroare, m[rimea ?a = a - a*
Se nume=te eroare absolut[ m[rimea:
? = ?a = a - a* (1.1)
Deoarece valoarea exact[ ,,a" este ]n general necunoscut[, eroarea absolut[ este =i ea ]n general
necunoscut[.
Se nume=te margine superioar[ a erorii absolute orice num[r R a ? ? care majoreaz[ eroarea
absolut[:
a
? = a - a* <= ? (1.2)
Avem evident:
a
*
a
a* - ? <= a <= a + ? (1.3)
Dac[ a?R , a != 0 , se nume=te eroare relativ[ m[rimea:
a
a a
a
- *
=
?
? = (1.4)
Se nume=te margine superioar[ a erorii relative orice num[r R a ? ? care verific[ relaia:
a ? <= ? (1.5)
Avem evident:
( ) a
a = a* 1+- ? (1.6)
Dac[ se cunoa=te o margine superioar[ a erorii absolute a ? atunci:
a
a
a a - ?
?
? = Analog, dac[ se
cunoa=te a ? , atunci:
a
a
a 1
a
- ?
?
? =
1.2. Surse principale de erori
Erorile care afecteaz[ un calcul numeric pot fi clasificate ]n cinci categorii.
Erori ale metodei
Studiul unui fenomen real se face pe baza unui model matematic asociat fenomenului. }n stabilirea
modelului matematic se fac anumite aproxim[ri sau idealiz[ri ale fenomenului care vor genera erori
ale metodei.
Erori de trunchiere
Apar atunci c`nd modelul matematic conine procese de trecere la limit[ sau calculul sumelor unor
serii. Deoarece un algoritm trebuie s[ conin[ un num[r finit de pa=i, calculul sumei unei serii, de
exemplu, se ]nlocuie=te cu suma unui num[r finit de termeni, gener`nd astfel o eroare de trunchiere.
Capitolul 1. Erori. Numere aproximative
1.2
Erori iniiale
Sunt datorate prezenei ]n modelul matematic a unor parametri care nu pot fi estimai exact. Cazul
tipic ]l constituie majoritatea constantele fizice.
Erori de rotunjire
Apar din cauza bazelor de numeraie diferite, utilizate ]n reprezentarea extern[ respectiv intern[ a
datelor. Reprezentarea extern[ utilizeaz[ ]n general baza 10. Reprezentarea intern[ a datelor este
]ntotdeauna ]n baza 2. Conversia din format extern ]n format intern conduce la apariia erorilor de
rotunjire.
Erori propagate
Apar ]n rezultatele operaiilor cu operanzi numere aproximative. Este evident c[, ]ntr-un calcul cu
numere aproximative, erorile iniiale ale operanzilor se propag[ ]n rezultat.
1.3. Reprezentarea numerelor aproximative
Dac[ a ?R , reprezentarea sa ]n baza 10 este de forma:
a 10 10 10m n 1
m n 1
m 1
m 1
m
m = ? + ? + + ? - + +
- +
-
- (1.7)
unde {0,1,2,3,4,5,6,7,8,9} i ? ? cu i?Z, sunt cifrele num[rului a.
0 m ? != se nume=te cifra rangului superior.
O aproximaie a* a num[rului ,,a" p[streaz[ un num[r finit de cifre din reprezentarea (1.7):
m n 1
m n 1
m 1
m 1
m
m
a* 10 10 10 - +
- +
-
- = ? + ? + + ? , m?Z, n?N (1.8)
m-n+1 ? se nume=te cifra rangului inferior.
Se nume=te cifr[ semnificativ[:
- orice cifr[ diferit[ de zero;
- un zero ]ncadrat de cifre semnificative;
- orice zero p[strat.
Toate cifrele reprezent[rii (1.8) se numesc cifre exacte (]n sens strict) dac[ eroarea absolut[ a
aproxim[rii nu dep[=e=te jum[tate din rangul inferior al aproximaiei:
* 10m n 1
2
? = a - a <= 1 ? - + (1.9)
Cifrele reprezent[rii (1.8) se numesc exacte ]n sens larg dac[:
? = a - a* <= 10m-n+1 (1.10)
1.4. Rotunjirea numerelor aproximative
Rotunjirea const[ ]n reducerea num[rului de cifre semnificative din reprezentarea zecimal[ a unui
num[r exact sau aproximativ. Pentru a se obine o eroare de rotunjire minim[, rotunjirea se face pe
baza urm[toarelor reguli:
- dac[ prima cifr[ eliminat[ este mai mic[ dec`t 5, cifrele p[strate r[m`n nemodificate;
- dac[ prima cifr[ eliminat[ este mai mare dec`t 5, se adug[ o unitate la cifra rangului inferior;
- dac[ prima cifr[ eliminat[ este 5 =i printre celelalte cifre eliminate exist[ cifre nenule, se adug[ o
unitate la cifra rangului inferior;
- dac[ prima cifr[ eliminat[ este 5 iar restul sunt nule, atunci (regula cifrei pare):
- dac[ ultima cifr[ p[strat[ este par[, cifrele p[strate r[m`n nemodificate;
- dac[ ultima cifr[ p[strat[ este impar[, se adug[ o unitate la cifra rangului inferior.
Capitolul 1. Erori. Numere aproximative
1.3
Leg[tura ]ntre eroarea relativ[ =i num[rul de ciftre exacte
Se poate demonstra c[ dac[ toate cifrele reprezent[rii (1.8) sunt exacte, atunci:
m
* 1 n 10
a
a a
?
<=
-
? =
-
(1.11)
Pentru n >= 2 , relaia anterioar[ devine:
m
* 1 n
2
10
a
a a
??
<=
-
? =
-
(1.12)
Dac[ cifrele sunt exacte ]n sens larg, estim[rile din relaiile (1.11) =i (1.12) se dubleaz[.
1.5. Erori propagate
}n acest paragraf sunt prezentate erorile propagate ]n cazul unor operaii elementare.
1.5.1. Eroarea unei sume
Preview document
Conținut arhivă zip
- Calcul numeric
- Cap1.pdf
- Cap2.pdf
- Cap3.pdf
- Cap4.pdf
- MetNum.pdf