Extras din curs
1. Să se studieze proprietăţile de mărginire, viabilitate, ciclicitate şi fără blocaje
pentru reţelele Petri ilustrare în figura următoare:
-a- -b-
Rezolvare.
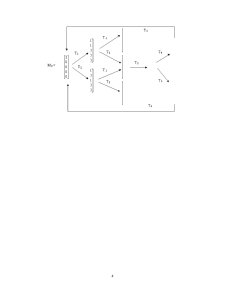
Graful de marcaje al reţelei din figura a) este :
Se observă că numărul de vectori de marcaj este finit, prin urmare reţeaua este mărginită.
Deoarece nici un marcaj nu este vector de blocaj reţeaua nu prezintă blocaje. Tranziţiile
T3 şi T4 se pot executa o singură dată. De aceea ele sunt cvasiviabile, spre deosebire de
celelalte tranziţii care se execută de un număr infinit de ori. În concluzie, se poate spune
că reţeaua este cvasiviabilă. Proprietatea de reversibilitate nu este îndeplinită deoarece nu
există o secvenţă de tranziţii care să conducă din marcajul M3 în marcajul iniţial.
Pentru reţeaua din figura b) cu ponderea arcului T4 P1 egală cu 2, graful de marcaje
accesibile este ilustrat în figura . Din graf se deduce că reţeaua este mărginită şi fără
blocaje ca cea dinainte, în plus, prin buclele care s-au format în graf, reţeaua este viabilă,
pentru oricare marcaj din graf şi oricare tranziţie putându-se găsi o secvenţă pornind de la
acest marcaj care să conţină tranziţia respectivă.
Pe acest exemplu se mai poate face o observaţie. Prin buclele care s-au format pe graf se
pot identifica secvenţele repetitive (secvenţe de tranziţii care, pornind de la un anumit
marcaj, conduc la acelaşi marcaj). Acestea sunt: S1 = T1T3T4, S2 = T1T1T2T2, S3 =
T1T1T2T3T4. Se poate vedea uşor că din toate marcajele accesibile de pe acest graf se
poate ajunge în marcajul iniţial, deci reţeaua este reversibilă.
Să consideram un ultim caz în care ponderea arcului T4 P1 este 3 (vezi figura -b-). În
acest caz se obţine următorul graf de acoperire:
T1, T2 T1, T2, T3, T4
Se observă că pe acest graf s-a substituit, conform algoritmului de construcţie a arborelui
de acoperire, valoarea 3 care s-ar fi obţinut după prima executare a lui T4 cu. În
continuare se poate observa că reţeaua Petri are toate poziţiile nemărginite; în acest fel se
deduce că reţeaua este nemărginită. Se păstrează însă proprietăţile de viabilitate şi de fără
blocaje.
Preview document
Conținut arhivă zip
- Probleme Retele Petri.pdf