Sisteme de Numerație

1 SISTEME DE NUMERAŢIE

Sistemele de numeraţie sunt ansambluri de reguli de reprezentare a numerelor cu ajutorul simbolurilor denumite cifre. Acestea pot fi poziţionale cum este sistemul zecimal şi nepoziţionale cum este sistemul roman. Într-un sistem poziţional de bază B un număr N cu parte întreagă şi parte fracţionară, separate prin punct (virgulă) se scrie sub forma următoare:

simbolurile bi sunt coeficienţii cu care se înmulţesc puterile Bi ale bazei în dezvoltarea polinomială a numărului pentru obţinerea valorii sale (exprimată în zecimal).

Pentru oricare sistem de numeraţie simbolul bazei sistemului se scrie cu cifrele unu-zero 10, iar numărul semnelor distincte pentru cifrele sistemului este egal cu B (de exemplu, pentru sistemul zecimal (0, 1, 2,..., 8, 9), B = 10 ; în sistemul de numeraţie binar (0,1), B = 2). Relaţia (1.2) explică de ce astfel de sisteme sunt denumite poziţionale; fiecare cifră bi, (din rangul i) intră în valoarea numărului respectiv cu o pondere dată de puterea „i" a bazei B.

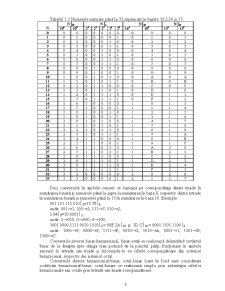
Fiecare număr se obţine din numărul anterior prin adăugarea unei unităţi la ultima cifră. În tabelul 1.1 sunt exprimate numerele naturale de la 0÷33 în sistemele de numeraţie cu baza B = 10, 2, 13, 16 (pentru fiecare poziţie scriindu-se şi puterea bazei).

La sistemele de numeraţie cu baza mai mică decât zece se utilizează tot semnele arabe (cele specifice pentru baza 10), iar la cele cu baza mai mare decât zece se introduc simboluri noi; de exemplu, pentru sistemul în baza 16 (hexazecimal) se introduc următoarele simboluri 10=A, 11=B, 12=C, 13=D, 14=E, 15=F.

Specificarea bazei în care sunt exprimate numerele există mai multe convenţii însă, în general, pentru baza 16 se adaugă litera H, iar pentru baza 8 se adaugă litera Q.

Există algoritmi (reguli) de conversie a unui număr dintr-o bază în alta. Algoritmul de conversie zecimal-binară, N|10 → N|2, pentru un număr întreg se deduce pornind de la expresia (1.2) sub forma:

00122332n2n1n1n2b21b2b2b2b2bN⋅+⋅+⋅+⋅++⋅+⋅=−−−−... (1.3)

Prin împărţiri succesive

unde:

şi b0 este rest

unde:

şi b1 este rest

unde:

şi bk este rest se obţin resturile care sunt tocmai biţii numărului N exprimat în binar, de exemplu 93|10→?|2

93=2⋅46+1→ bn-7 = 1

46=2⋅23+0→ bn-6 = 0

23=2⋅11+1→ bn-5 = 1

11=2⋅ 5+1→ bn-4 = 1

5=2⋅ 2+1→ bn-3 = 1

2=2⋅ 2+0→ bn-2 = 0

1=2⋅ 0+1→ bn-1= 1 1001234569321202121212021=⋅+⋅+⋅+⋅+⋅+⋅+⋅=N

Astfel: 210101110193=

Algoritmul de conversie zecimal-binară, N|10 → N|2, pentru un număr fracţionar (subunitar) se deduce pornind de la expresia: mmmmbbbbbN−−−−−−−−−−−−⋅+⋅++⋅+⋅+⋅=22...222)1()1(3322112 (1.5)

Prin înmulţiri succesive cu 2

unde:

se obţin părţi întregi (0 sau 1) care sunt tocmai biţii numărului N exprimat în binar, de exemplu 210?48932.0=. Înmulţirea se opreşte când partea fracţionară devine zero sau când se consideră satisfăcător un număr de cifre binare pentru precizia stabilită.

0.48932 × 2 = 0 + 0.97864 → b-1 = 0

0.97864 × 2 = 1 +0.95728 → b-2 = 1

0.95728 × 2 = 1 +0.91456 → b-3 = 1

0.91456 × 2 = 1 +0.82912 → b-4 = 1

0.82912 × 2 = 1 +0.75824 → b-5 = 1

0.75824 × 2 = 1 +0.51648 → b-6 = 1

0.51648 × 2 = 1 +0.03296 → b-7 = 1 210...0111111.048932.0= 10165432148932.0...21212121212120=+⋅+⋅+⋅+⋅+⋅+⋅+⋅=−−−−−−−N

Pentru conversia zecimal-binară a unui număr ce prezintă atât parte întreagă, cât şi parte fracţionară se combină cei doi algoritmi. Din exemplele de mai sus s-a putut vedea că pentru conversia binar-zecimală, N|2 → N|10, se adună puterile succesive ale lui 2, fiecare fiind înmulţită cu bitul din poziţia respectivă a numărului binar. Algoritmii deduşi mai sus (1.4) şi (1.6) pot fi aplicaţi şi în cazul conversiei zecimal-octal, zecimal-hexazecimal etc.

Conversiile directe octal-binar, hexazecimal-binar, cât şi conversiile inverse binar-octal, binar-hexazecimal se realizează mult mai simplu datorită faptului că 8 şi 16 sunt puterile lui doi (23, 24). Un număr (mai mic decât baza) în octal şi în hexazecimal poate fi exprimat prin trei cifre binare (triadă) respectiv prin patru cifre binare (tetradă).