Technici Euristice

Automate finite.

Rolul lor în modelarea activităţilor din analiza lexicală[1]

Un program de recunoastere pentru un limbaj este acel program care primeste la

intrare un sir “X” si răspunde “DA” dacă “X” este o secvenţă a limbajului, respective“NU”, în

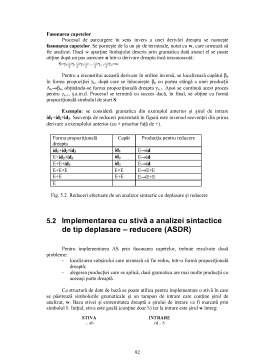
caz contrar. Pentru a analiza programul de recunoastere corespunzător unei expresii regulate

(program gen analizor lexical) trebuie contruită, în prealabil, o diagramă de tranziţii

generalizată numită automat finit (AF).

Un AF poate fi determinist (AFD) sau nedeterminist (AFN). Nedeterminarea constă,

în principiu, în faptul că, din cel puţin o stare sunt posibile mai multe tranziţii pentru acelasi

simbol de intrare.

Atât AFD cât si AFN pot recunoaste limbaje specificate prin expresii regulate. De

obicei AFD conduc la programe mai rapide dar numărul lor de stări este mai mare.

Există metode de transformare (conversie) a expresiilor regulate în ambele tipuri de

automate. Conversia este mai simplă în cazul AFN.

În exemplele ce urmează în acest paragraf se va utiliza următoarea expresie

regulată[1]:

(a|b)*abb – mulţimea tuturor sirurilor compuse din caractere a si b care se termină

cu secvenţa abb (ex: abb, aabb, babb, aaabb, )

1.1 Definiţia unui AFN

Un AFN este un model matematic reprezentat prin următorul cvintet:

AFN = <S,A,ft,so,F>, unde:

- S este mulţimea stărilor;

- A reprezintă mulţimea simbolurilor de intrare (alfabetul de intrare);

- ft se numeste funcţie de tranziţie si pune în corespondenţă perechi „staresimbol”

cu ”stări”, adică: ft : S x A -> S ;

- so este starea iniţială (de start); soÎS;

- F este mulţimea stărilor finale (acceptoare); F Í S.

Un AFN se poate reprezenta ca un graf orientat etichetat numit graf de tranziţie în

care nodurile corespund stărilor automatului iar etichetele descriu funcţia de transfer (ft). Se

poate remarca asemănarea dintre un graf de tranziţie si o diagramă de tranziţie. Deosebirile

de principiu sunt următoarele:

- acelasi caracter se poate utiliza pentru a eticheta două sau mai multe tranziţii din

aceasi stare;

- este permisă utilizarea ca etichetă a simbolului ε (sirul vid).

În fig. 1.1 se prezintă un exemplu de AFN corespunzător expresiei regulate:

(a|b)*abb. Nedeterminismul se manifestă în starea 0 în care, pentru simbolul de intrare a,

sunt posibile 2 tranziţii: se poate rămâne în starea 0 sau se poate trece în starea 1.

Fig. 1.1 Un prim exemplu de AFN pentru expresia: (a|b)*abb

În calculator, funcţia de tranziţie se poate implementa în mai multe moduri. O

modalitate potrivită este sub forma unei tabele de tranziţii care au câte o linie pentru fiecare

stare, câte o coloană pentru fiecare simbol de intrare (inclusiv pentru simbolul ε, daca este

necesar) (fig. 1.2). Intrarea în tabelă corespunzătoare liniei i si simbolului de intrare a este

mulţimea de stări pentru care există tranziţii din starea i etichetate cu simbolul a.

Stare Simbol intrare

a b

0 {0,1} {0}

1 - {2}

2 - {3}

3 - -

Fig 1.2 Tabela de tranziţii corespunzătoare AFN din fig. 1.1

Se spune că un AFN acceptă un sir de intrare ”X” dacă si numai dacă există un drum

în graful de tranziţii începând din starea de start până la o stare acceptoare astfel încât

etichetele pe drumul respectiv să formeze sirul ”X”. Drumul respectiv se numeste cale de

acceptare pentru sirul ”X”. Aceluiasi sir de intrare îi pot corespunde mai multe căi de

acceptare într-un AFN. Totalitatea sirurilor acceptate de un AFN reprezintă limbajul definit

de automatul respectiv.

1.2 Definiţia unui AFD

Un AFD este un caz particular de AFN la care se impun următoarele restricţii asupra

funcţiei de transfer ft.

1) din nici o stare nu pleacă tranziţii etichetate cu ε;

2) pentru orice stare s si pentru orice simbol de intrare a, există cel mult un arc etichetat

cu a care pleacă din s.

În concluzie, un AFD va avea cel mult o tranziţie din fiecare stare pentru orice simbol de

intrare. Aceasta înseamnă ca AFD conţine cel mult o cale de acceptare (recunoastere) pentru

un sir de intrare dat.

În fig. 1.3 se prezintă