Extras din curs
Application nb.1
Surveying calculations
The ensemble of operations in order to obtain plans and maps is known as surneying.Because during land surveying, the calculations involve a large volume of work, it is proper that the way of doing these calculations to be well studied.
Application theme
In order to establish the position of points, depending on a reference coordinates system, related to the Earth’s surface, it is necessary the knowledge of some essential surveying calculations.
Datums
1. The space rectangular coordinates of the 32 and 43 points from the triangulation network.
2. The results of measurements for establishing the space position of a new point, 107: the horizontal angle, β, the zenith angle, Z, the ground distance, di, which is measured directly using a 50 m long steel measuring tape.
43 Δ
(X43, Y43, Z43)
β
Δ di , Z o
32 107
(X32, Y32, Z32)
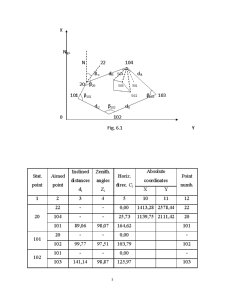
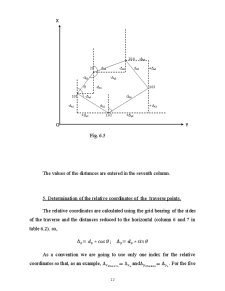
Fig. 1.1
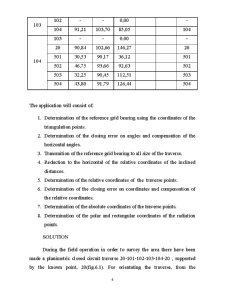
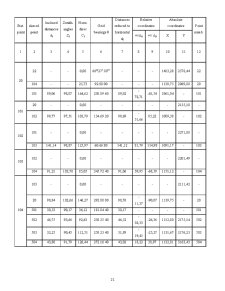
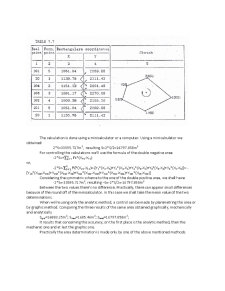
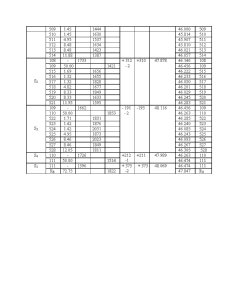
The applications datums containg the initial elements i. e. , space rectangular coordinates of the 32 and 43 points, and the elements resulting from field measurements as the horizontal and zenith angles and the ground distance are indicated in table.
NOTE: The datums of the application will be modified as below: the abscisa of the 32 point: X32 +/-n(m) the ground distance: di +/-n(m)
Table 1.1
Pct.
statie
Pct.
vizat
Distanta
Inclinata
di
Unghi
Zenital
Z
Unghi
Orizontal
β
Coordonate spatiale
X Y Z
Nr.
pct.
45
51
101
-
138.75
-
94g51c
-
131g74c
2421,69 1833,12 231,96
1735,43 2351,12 164,55
43
32
The application will consist of :
1. Determination of the grid bearing and horizontal distance of 32 – 43 its coordinates .
2. Determination , by transfer, of the 32 – 107 direction’s grid bearing .
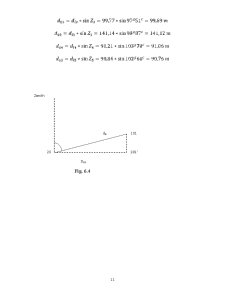
3. Determination of the distance reduced to the horizontal do and the level difference between the known point , 32 and the new one , 107 .
4. Determination of the relative plane rectangular coordinates x and y of the 107 point .
5. Determination of the space rectangular coordinates of the 107 point .
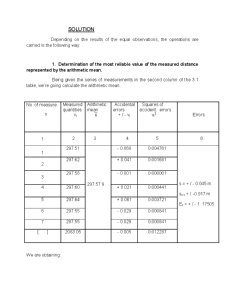
Solution
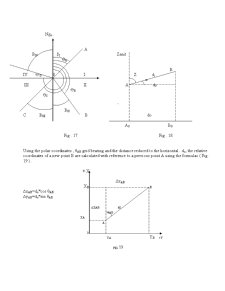
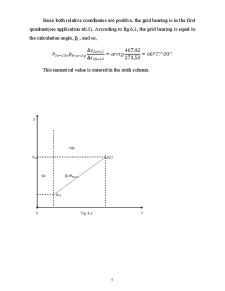
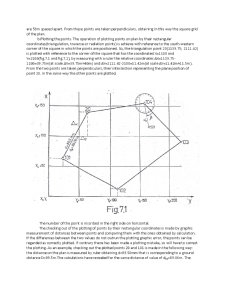
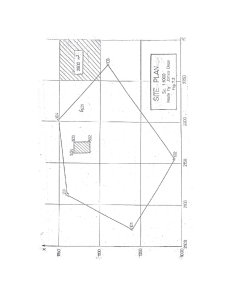
The topographic plan is an orthogonal projection . The points position on the plan is established in a plane rectangular coordinates system . For Romania , according to the stereographic projection 1970 , the general plane rectangular coordinates system was obtained considering the abscisa X as the plane projection of the central point’s meridian situated north of Fagaras (Ngo) , and the ordinate Y perpendicularly on the abscisa in the central point (fig . 1. 2 ) . This way the coordinates axis have the same orientation as the cardinal points (the X axis on S – N direction and Y axis on W – E direction.) .
In the conformal traverse cylindrical projection (Gauss’ s projection) , the X axis is represented by the plane projection of the central meridian , and the image of terrestrial equator in the form of a straight line at right angle to the axial (central) meridian serves as Y axis.
In the zonal system, the origin of coordinates for all points in the given zone is assumed to the intersection of the central meridian with the equator . ( fig . 1. 3 ).
In surveying the direction according to which all the directions in field are determinated is represented by the north ( N ) direction .
On the Earth’s surface , through every point we have a certain geographical ( or true ) meridian that has a stable position and a certain magnetic meridian which is not stable in time .
As a reference direction we will take a parallel to the geographical meridian of the central point ( in the case of stereographic projection ) and to the central meridian ( in the case of Gauss’s projection ) . This way , the grid bearing of a direction of line A-B , written θAB , is used to obtain the direction of line A-B with reference to the central meridian , or to a line parallel to it .
The grid bearing is reckoned clockwise from the central meridian or from a line parallel to it up to the direction , of a given line within 0g to 400g ( or 0o to 350o)
Preview document
Conținut arhivă zip
- Land Surveying - Surveying Calculus.pdf