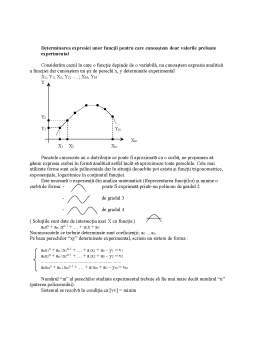
Extras din curs
A, B – puncte de extrem
+ minim
- maxim
f(x) = x2
f’(x) = 2x
f’’(x) = 2
Dacă avem o funcție de mai multe variabile f(x1, x2, , xn) condiția de a fi un punct de extrem se scrie sub forma unui sistem:
Există posibilitatea ca toate derivatele să se anuleze și totuși să nu fie un punct de extrem ci o zonă staționară, acest lucru se determină tot prin derivare de ordinul II și anume dacă derivatele de ordinul II sunt nule avem de-a face cu un punct staționar.
f’(x) = 0 – punct staționar
Extreme condiționate ale funcțiilor
În unele situații se impun condiții suplimentare iar punctul căutat trebuie să atingă un minim sau un maxim dar cu respectarea condițiilor impuse. Dacă se cere aflarea unui extrem pentru o funcție de mai multe variabile f(x1, x2, , xn) și dacă se impun următoarele condiții:
g1(x1, x2, , xn) = 0
g2(x1, x2, , xn) = 0
gk(x1, x2, , xn) = 0
atunci se scrie ecuația Euler-Lagrange de forma:
f = f(x1, x2, , xn) - l1* g1(x1, x2, , xn) - l2* g2(x1, x2, , xn) - - lk* gk(x1, x2, , xn)
l1, l2, , lk – coeficienți necunoscuți în prima fază dar care pot fi determinați din sistemul următor:
Rezultatul acestui sistem ne conduce și la soluția căutată și anume acel rezultat x1, x2, , xn pentru care sunt îndeplinite condițiile g1, g2, ,gk
- x1, x2, , xn
- l1, l2, , lk
n + k necunoscute
Sistemul de „n” ecuații de forma și k ecuații de condiții
Exemplu:
h r, h = ?
r
Varianta 1: - pentru un volum dat V = c1
se cere aria minimă
funcția este : f(R,h) = 2pR2 + 2pRh - aria
g1(R,h) = pR2h – c1 = 0
Ecuația Euler-Lagrange este :
F = 2pR2 + 2pRh - l(pR2h – c1)
= 0
= 0
= 4pR + 2ph - 2lpRh = 0 (1)
= 2pR - lpR2 = 0 (2)
din (1) rezultă :
2R + h - lRh = 0
din (2) rezultă :
2 - lR = 0
Þ l =
2R+h - Rh = 0
2R + h – 2h = 0 Þ 2R – h = 0
Þh = 2R
înlocuind în g1 Þ R, h
Varianta 2: - pentru aria dată A = c2
V = maxim
f(R,h) = pR2h - volumul
g1(R,h) = 2pR2 + 2pRh – c2 = 0
Preview document
Conținut arhivă zip
- Topografie.doc
Alții au mai descărcat și
Generalitati Granulozitatea, adica textura reprezinta repartitia procentuala, dupa marimea lor, a granulelor componente ale fazei solide ale...
Se prezintă proiectarea unui planşeu intermediar al unei clădiri de locuit P+1E, cu dimensiunile în plan 9,05 x 9,05 metri şi înălţimea nivelului...
Stabilizarea solului cu lianți hidraulici rutieri este o metodă care a dovedit, în timp, eficiența executarii fundațiilor din materiale coezive și...
Tarile romane, partea extracartpatica au fost pe parcursul intergului secol XVIII conduse de domni fanarioti, sistem inaugurat in 1716 si care a...
TEMA NR.1 Sa se verifice stabilitatea la alunecare a versantului stances din figura , avand 2 sisteme principale de fisurare cu inclinari de 20...
Domeniul de utilizare a fişei tehnologice. Fişa tehnolgică este elaborată la executarea scheletului monolit şi umpluturii din zidărie din blocuri...
Te-ar putea interesa și
1.)TEODOLIT ELECTRONIC Seria DT Aplicatii Teodolitul electronic seria DT are un sistem incremental optic de citire a unghiurilor cu ajutorul...
CAPITOLUL I AMPLASAREA GEOGRAFICA SI LOCALIZAREA OBIECTIVULUI PROIECTAT 1.1 C. V. Localitatea Baru este situată în partea sudică a județului...
1. Introducere Conform etimologiei cuvantului (din limba greaca, topos = loc si graphien = a desena, a scrie), Topografia este una din stiintele...
1.)TEODOLIT ELECTRONIC Seria DT Aplicatii Teodolitul electronic seria DT are un sistem incremental optic de citire a unghiurilor cu ajutorul...
Capitolul I Localizarea geografică şi economico – administrativă 1.1. Localizarea perimetrului. Perimetrul de exploatare Petrila este situat în...
Cap.1 Lucrari topografice la proiectarea constructiilor industrial si civile. 1.1.1. Retele de sprijin topografice legate de proiectarea...
1. Scopul topografiei. Definitie Topografia este o ramura a geodeziei care se ocupa cu tehnica masuratorilor unei portiuni a scoartei Pamantului,...
§1. Noţiuni generale despre topografie şi cartografie Harta se utilizează în multe activităţi umane, fiind folosită mai ales în cercetările...