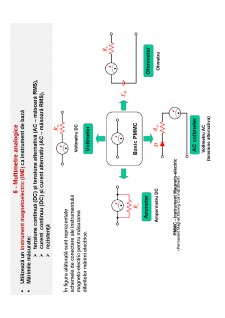
Extras din curs
Exemplu de schemă bloc a unui aparat digital (aparat bazat pe procesarea numerică a semnalelor achiziționate)
Dispozitiv de eșantionare + Convertor Analog/Digital
Memorie
Procesor
Semnal de intrare analogic
Semnal discret
Semnalul purtător al informației de măsurare (semnal metrologic) este de cele mai multe ori semnal analogic. Aparatele de măsurare numerice (digitale) și sistemele de calcul, procesează informațiile numai sub formă numerică, motiv pentru care după o eventuală condiționare a acestora este necesară conversia analog-digitală (numerică).
Conversia analog-digitală (A/D) este procesul prin care unui semnal analogic i se asociază o secvență de coduri numerice compatibile cu structura internă a aparatelor de măsurare digitale și a calculatoarelor.
1
Etapele conversiei A/D 2
Pentru a putea fi acceptate de calculator în vederea prelucrării numerice semnalele analogice trebuiesc convertite în semnale numerice. În cadrul acestei conversii semnalul analogic este supus la trei operații succesive:
- eșantionarea,
- cuantizarea
- codarea
(a) Semnalul analogic care urmează să fie convertit (tensiune care variază în timp). (b) Etapa I-a (S/H): eșantionează și memorează (sample and hold). In cadrul acestei etape singura informație reținută este valoarea instantanee corespunzătoare momentului eșantionării
3
(c) Etapa II-a: cuantizare In cadrul acestei etape valoarea instantanee este convertită în numărul întreg cel mai apropiat (d) Diferența dintre semnalul eșantionat (b) și cel cuantizat (c) este egală cu eroarea de cuantizare care se încadrează în intervalul LSB21±. LSB - Least Significant Bit (desemnează distanța dintre două niveluri consecutive de cuantizare)
4
5
Eșantionarea (discretizarea în timp a semnalului analogic)
Prin eșantionare se înțelege operația de transformare a unui semnal continuu variabil, x(t) într-un semnal discret în timp, format dintr-o succesiune de impulsuri foarte scurte numite eșantíoane, ale căror amplitudini sunt egale cu valoarea semnalului din momentul de eșantionare (figura b). Prin urmare, eșantionarea reprezintă modularea impulsurilor în amplitudine și se realizează prin înmulțirea semnalului cu o succesiune de impulsuri foarte scurte, în cazul ideal - impulsuri Dírac (cu durata 0 si amplitudinea infinită)
Eșantionarea se realizează cu frecvența de eșantionare fE impusă de generatorul de tact
Cuantizarea (discretizarea valorii instantanee a eșantionului) este operația prin care eșantioanelor prelevate de dispozitivul eșantionator li se asociază semnale de aceeași natură, dar cu amplitudinea bine determinată. Pentru aceasta, domeniul de variație al semnalului analogic de intrare este împărțit într-un anumit număr de subdomenii (cuante), de obicei egale între ele. Dispozitivul de cuantizare va stabili în urma unei corelații prestabilite cîte subdomenii cumulate corespund eșantioanelor de amplitudine prelevate și implicit, ce amplitudine vor avea semnalele de la ieșirea sa.
Deci, în urma eșantionării și cuantificării, unui semnal analogic cu o infinitate de valori în domeniul său de variație i se va atribui o mărime analogică de aceeași natură, dar cu un număr prestabilit de valori.
6
CAN sau Convertor Analogic Numeric reprezintă un bloc sau un circuit care poate accepta o mărime analogică (curent, tensiune) la intrare, furnizând la ieșire un număr care constituie o aproximare (mai mult sau mai puțin exactă) a valorii analogice a semnalului de la intrare. Spre deosebire de o mărime analogică ale cărei valori se pot găsi în orice punct din domeniul său de variație, mărimea numerică (sau digitală) posedă numai o variație în trepte. Astfel, întreg domeniul de variație este divizat într-un număr finit de „cuante” (trepte elementare) de mărime determinată de rezoluția sistemului, în acest mod, diferența între cele mai apropiate valori numerice nu poate fi făcută mai mică decât această treaptă elementară, ceea ce face ca, principial, reprezentarea informației sub forma numerică să fie legată de introducerea unei erori, numită eroare de cuantizare.
Conversia A/D se realizează cu dispozitive fizice specifice:
-
Circuite de eșantionare - memorare (sample and hold, circuite S/H)
-
Circuite de conversie A/D care asigură cuantizarea și codarea Ansamblul acestor circuite formează un CAN - Convertor Analog Numeric
Etapa (1) a conversiei A/D - eșantionarea, aspecte teoretice
Eșantionarea unui semnal analogic x(t), continuu variabil în timp, constă în prelevarea valorilor semnalului la momente de timp echidistante, nTe, obținându-se o succesiune de valori discrete - eșantioane de amplitudine. Rezultatul eșantionării uniforme a unui semnal continuu x(t) este un șir de eșantioane x[nTe],unde Te este intervalul de timp între două eșantioane și se numește perioadă de eșantionare
Reprezentarea grafică a unei secvențe
Secvențe speciale
Semnalul discret este reprezentat matematic printr-o secvență (șir) de valori
xe = {x(n)} cu n = -N...+N
x(n) fiind eșantionul de rang n din secvență
Funcția DELTA unitate
()()()≠==⋅−δ⋅−δ=δΣ∞−∞=eeeneTenTtpentrunTtpentruTntTntt01
Funcția DELTA periodică
Reprezintă o succesiune de impulsuri unitate, plasate echidistant pe axa timpului, la intervale egale cu Te (perioadă de eșantionare) în (s) 1/Te = fe (frecvența de eșantionare) în Hz sau eșantioane/s 7
Eșantionarea ideală - matematic se exprimă prin înmulțirea semnalului analogic cu funcția DELTA periodică
()()()eneenTtnTxtx−δ⋅=Σ∞−∞=
-
Semnalul rezultant are aceeași valoare instantanee cu semnalul analogic pentru momente de timp egale cu nTe (n - număr întreg) și este egal cu 0 în rest. Informația preluată de semnalul discret din structura semnalului analogic pe care îl reprezintă, depinde de perioada de eșantionare.
-
Pentru ca semnalul discret să reprezinte în mod ideal semnalul analogic, perioada de eșantionare Te ar trebui să fie infinit mică (la limită egală cu zero). În realitate, perioada de eșantionare are o valoare finită care depinde de arhitectura convertorului A/D deci semnalul discret poartă mai puțină informație decât cel analogic.
-
Problema care trebuie rezolvată: care este criteriul în baza căruia se poate alege perioada de eșantionare pentru obținerea unei eșantionări corecte Eșantionare corectă: un semnal analogic este corect eșantionat dacă el poate fi reconstruit pornind de la reprezentarea sa numerică.
Preview document
Conținut arhivă zip
- Mijloace de masurare.pdf
- Semnale numerice.pdf