Comenzi Numerice

Capitolul 1

1.1. Schema de bază a controlului numeric

1.2. Ecuaţii lineare în diferenţe

1.1Schema de bază a controlului numeric.

Controlul sistemelor fizice, realizat cu ajutorul calculatorului digital a devenit din ce în ce mai evident. Dezvoltarea în domeniul logicii digitale folosită în controlul proceselor a fost generată în bună masură de creşterea flexibilităţii programelor de control reuşindu-se astfel o dinamică a proceselor de control simultan cu îndeplinirea de noi cerinţe impuse sistemului. În principal şi istoriceşte privind aceste succese se datoreazǎ topologiei cu reacţie (feedback) introdusă în mod special de lucrările lui BODE şi NYQUIST.

Topologia tipică şi actuală a sistemului de bază care permite controlul răspunsurilor dinamice ale diverselor sisteme este prezentată în figura 1.1.

Fig.1.1.Schema controlului numeric.

Figura 1.1. permite introducerea urmatoarelor notaţii de baza, care sunt folosite in decursul acestui curs.

r - referinţa sau comanda de intrare

u - comanda cu care se realizează conducerea procesului

y - mărimea controlată sau mărimea de ieşire

ŷ - mărimea de reacţie – ieşirea unui sensor sau o aproximaţie a lui y numită marime estimată

ê = r - ŷ - mărimea de eroare actuală

e = r - y - mărimea de eroare a sistemului

w - perturbaţia ce actionează din exterior asupra instalaţiei tehnologice

v - perturbaţia ce actionează asupra traductorului

A/D - conversie analog-digital

D/A - convenţie digital-analog

O funcţionare “satisfăcătoare” a sistemului din fig.1.1 presupune forţarea mărimii y(t) să urmăreasca variatia mărimii r(t), în ciuda prezenţei perturbaţiilor exterioare w(t) si v(t).

Este de asemenea de dorit ca procesul de urmărire a lui r(t) de către y(t) să se producă în condiţiile în care dinamica instalaţiei tehnologice se modifică. Procesul de apropriere a lui y(t) de r(t), chiar şi în cazul r≡0 este denumit un proces de reglare.

Dacă sistemul are o bună reglare în prezenţa perturbaţiilor se spune despre sistemul de control că prezintă o rejecţie a perturbaţiilor. Sistemul de control avand o bună reglare la modificarea parametrilor procesului este caracterizat drept un sistem de sensitivitate redusă la aceşti parametrii.

Sistemul avand o bună rejecţie a perturbaţiilor simultan cu o sensitivitate redusă la perturbaţii se denumeşte un sistem robust.

Problema controlului care a fost discutată mai sus nu se limitează numai la comanda numerică. Totuşi se poate considera că schema din fig. 1 este cea care asigură un control continuu al proceselor industriale.

Referitor la schema din fig.1.1, merită o discuţie dispozitivul A/D – convertor analog digital. Fizic acest dispozitiv primeşte la intrare un semnal electric (de obicei acesta este o tensiune electrică) şi generează la ieşire o secventă numerică. De obicei, ieşirea sensorului, sau ieşirea estimatorului de mărime de ieşire , suportă procedeul de eşantionare în procedeul de prelucrare propriu A/D cu scopul construcţiei erorii de reglare în interiorul calculatorului digital. Se va face ipoteza ca procesul de formare a erorii este periodic, de perioada T, numită perioada de eşantionare. Periodicitatea acestei construcţii de eroare este realizată prin semnale de intrerupere generate de către CEAS.

Intreruperile generate de către U.C. a computerului trebuiesc generate după ce acesta execută toate codurile de execuţie. O asemenea funcţionare a sistemului din fig. 1 se numeşte funcţionare ciclică (free running). Este posibila si o altă funcţionare, în care cererea de întrerupere să fie condiţionată si fixată de lungimea codului de executat.

În concluzie: există o anumită periodicitate în execuţia eşantionărilor şi conversiei A/D în semnale digitale, proces care introduce clasa de semnale discrete. Deasemenea în sistem pot fi regăsite semnale de tip continuu precum w şi y. Un sistem care prezintă ambele categorii de semnale se numeşte un sistem de eşantionare a datelor.

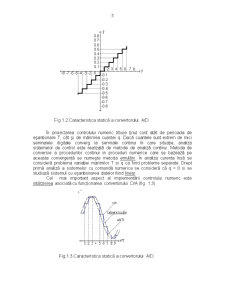
Simultan cu generarea de semnale discrete, convertorul A/D generează semnale de cuantificare. Evidenţa acestor semnale este datorată caracteristici statice a convertorului A/D din fig.1.2. De observat că procesul de cuantizare este nelinear. Un semnal care este simultan discret si cuantificat se numeşte semnal digital. ŷ(t)

Fig.1.2.Caracteristica statică a convertorului A/D.

În proiectarea controlului numeric trbuie ţinut cont atât de perioada de eşantionare T, cât şi de mărimea cuantei q. Dacă cuantele sunt extrem de mici semnalele digitale converg la semnale continui în care situaţie, analiza sistemelor de control este realizată de metode de analiză continui. Metoda de conversie a procedurilor continui in proceduri numerice care se bazează pe aceasta convergenţă se numeşte metoda emulării. În analiza curenta însă se consideră problema variaţiei marimilor T si q ca fiind probleme separate. Drept primă analiză a sistemelor cu comandă numerica se consideră că q = 0 si se studiază sistemul cu eşantionarea datelor fiind linear.

Cel mai important aspect al implementării controlului numeric este intârzierea asociată cu funcţionarea convertorului D/A (fig. 1.3)

Fig.1.3.Caracteristica statică a convertorului A/D.

Fiecare valoare a lui u(kT) este menţinută constantă pană la generarea de către computer a unei noi valori. În acest mod valoarea continuă a lui u(t) – care constituie din salturi discrete, sau matematic vorbind u(t) acuză o variaţie de tip scara – anticipează cu T/2 variatia valorii medii, reprezentată in fig.3.1. cu linie punctată.

Dacă se foloseste analiza continuă precizată anterior (q = 0), atunci dacă se introduce o intârziere de T/2 se obţin rezultate foarte bune.