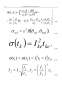Controlul Vectorial al Acționărilor Electrice

I. Interacţiunea magnetică

I.1. Câmpul magnetostatic

Interacţiunile magnetice sunt cunoscute din antichitate, de exemplu atracţia magnetitei

(Fe3O4 - întâlnită sub formă de minereu) asupra fierului. Numele de magnetism provine de la

orăşelul antic Magnesia unde, conform tradiţiei, s-a observat pentru prima dată fenomenul.

Interacţiunea magnetică, spre deosebire de cea gravitaţională, nu se manifestă la toate

corpurile. În cazul magneţilor naturali sau obţinuţi artificial, acţiunea magnetică este mai

concentrată în anumite domenii, numite poli magnetici.

Orice magnet are cel puţin o pereche de poli (polul nord şi polul sud), formând astfel un

dipol magnetic. Polii magnetici singulari (monopolii) nu s-au întâlnit încă. Chiar şi ruperea

unui dipol (de exemplu spargerea unei bare magnetice) nu conduce la obţinerea de monopoli,

ci dă naştere la doi dipoli magnetici. Polii magnetici de acelaşi fel se resping, cei de nume

diferite se atrag. În câmpul magnetic al Pământului, magneţii în formă de bară care au

posibilitatea de rotire (ac magnetic) se orientează astfel încât polul nord al magnetului să

indice nordul geografic. Polul nord geografic al Pământului este deci un pol magnetic sud şi

invers.

Geometria câmpului unui dipol magnetic se poate descrie ca şi în cazul unui dipol electric

(o formaţiune neutră din punct de vedere electric compusă din două sarcini punctiforme egale

şi de semn contrar care se află la o distanţa l una faţă de alta) prin linii de câmp a căror

configuraţie se poate evidenţia prin acţiunea de orientare exercitată de câmpul magnetic

asupra unor particule magnetice lunguieţe (de exemplu pilitură de fier). Sensul pozitiv al

liniilor magnetice de câmp s-a convenit a fi de la nord la sud.

Câmpul creat de magneţii permanenţi, (fig.1), se numeşte câmp magnetostatic.

Fig.1.Câmpul unui dipol magnetic realizat cu ajutorul unui magnet permanent

Bara magnetică exercită o forţă (cuplu) asupra acului magnetic (care este de fapt un alt

magnet) astfel încât în echilibru el se aliniază pe o direcţie particulară, paralelă cu direcţia

câmpului.

I.2. Câmpul magnetic staţionar

În afară de magneţii permanenţi, câmpurile magnetice sunt create şi de curenţi electrici.

Curenţii electrici constanţi în timp şi spaţiu realizează câmpuri magnetice staţionare. Cauza o

constituie sarcinile electrice în mişcare (electronii). Liniile magnetice de câmp al unui

conductor liniar parcurs de curent sunt cercuri concentrice având conductorul drept axă

(fig.2). În fig.2.a. se prezintă orientarea piliturii fine de fier de-a lungul liniilor de câmp create

de conductorul liniar parcurs de curent. Evident că acest câmp trebuie să fie suficient de

puternic astfel încât forţa exercitată asupra piliturii de fier să învingă forţa de frecare dintre

pilitură şi suportul de susţinere (de exemplu hârtie). Aproape de conductor, unde câmpul

magnetic este puternic, forţa exercitată asupra piliturii este suficient de mare pentru a o putea

orienta, astfel încât liniile de câmp să devină vizibile. Însă pe măsură ce distanţa de la

conductor creşte câmpul magnetic se diminuează, existând astfel un punct de la care pilitura

de fier nu mai poate fi orientată, forţa de frecare fiind mai mare decât cea exercitată de

Controlul vectorial al acţionărilor electrice

câmpul magnetic. Sensul liniilor magnetice de câmp se află, cunoscând direcţia curentului, cu

ajutorul regulii burghiului drept (fig.2.b).

Fig.2. Câmpul magnetic staţionar creat de un conductor parcurs de un curent constant

În cazul în care conductorul parcurs de curent formează o spiră se obţine un câmp

magnetic având geometria prezentată în fig.3.

Fig.3. Câmpul magnetic staţionar creat de o spiră parcursă de un curent constant

Câmpul magnetic al unei bobine cilindrice (numită şi solenoid), fig.4, este omogen în

interiorul ei, în timp ce în exteriorul bobinei acesta este asemănător câmpului magnetic al unui

dipol (fig.1) şi faţă de intensitatea câmpului din interior intensitatea în exterior este mai mică,

atât timp cât lungimea l a bobinei este mare în comparaţie cu diametrul bobinei.

Fig.4. Câmpul magnetic staţionar creat de o bobină parcursă de un curent constant

Linii de câmp magnetic asemănătoare celor din fig.4. pot fi obţinute şi cu ajutorul unui

bare magnetice cilindrice (fig.5).

Observaţie

Câmpul electrostatic este generat de sarcini electrice elementare în repaus. În cazul

câmpului electrostatic, sarcinile electrice pozitive şi negative sunt surse şi locuri de dispariţie

ale unui câmp electric. Liniile de câmp electric încep şi se termină totdeauna pe sarcini

electrice. În câmp magnetic nu există sarcini magnetice elementare ca surse de câmp

magnetic, respectiv ca origine a liniilor câmpului magnetic. Liniile de câmp magnetic sunt

linii mereu închise; în cazul magneţilor permanenţi liniile de câmp exterioare trebuie

considerate ca închizându-se în interiorul magneţilor. Acest lucru este confirmat prin

spargerea unui magnet, ocazie cu care iau naştere doi noi poli magnetici.