Extras din document
Introducere
De ce metode numerice de calcul?
- Ecuaţiile diferenţiale cu derivate parţiale sunt
neliniare sau nu pot fi liniarizate fără a se
afecta soluţia;
- Domeniul pe care se face calcul este
complex;
- Condiţiile pe frontieră sunt de tip mixt şi/sau
dependente de timp;
- Mediul este neomogen şi/sau anizotrop.
Rezolvarea unei probleme cu ajutorul metodei
diferenţelor finite implică trei etape:
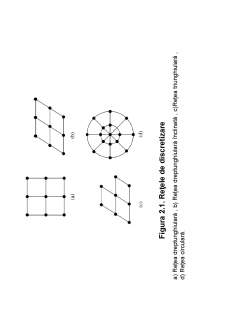
- Discretizarea - divizarea domeniului analizat
într-o reţea de noduri în care se va calcul
soluţia;
- Aproximarea derivatelor ecuaţiilor diferenţiale
corepunzătoare nodurilor reţelei de
discretizare prin scheme cu diferenţe finite;
- Rezolvarea sistemului de ecuaţii format
ţinând cont de condiţiile pe frontieră (la limită)
şi/sau condiţiile iniţiale.
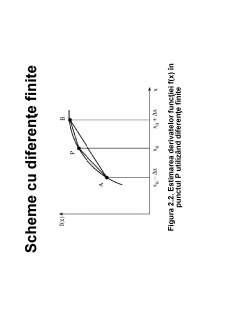
( ) f ( x0 + Δx) − f ( x0 )
′
Formula cu diferenţă înainte (forward-difference)
) 0 0
0
x x x
f x
x
Δ
Δ
????
f ( x ) − f ( x − Δx)
Formula cu diferenţă înapoi (backward-difference)
( ) ) 0 0
0
x
f x
x
Δ
′
Δ
????
Formula cu diferenţă centrală (central-difference)
f ( Δ ) f ( ) ( ) 0 0
0 2
x x x x
f x
x
+ − −Δ
′
Δ
????Aplicarea metodei diferențelor finite ecuațiilor eliptice
conduce la un sistem foarte mare de ecuații algebrice, a
cărui rezolvare este o problemă în sine.
Cele mai utilizate metode pentru rezolvarea acestui sistem
sunt: Metode pentru matrici bandă și Metode iterative.
Metode pentru matrici bandă
1
- Metoda de eliminare a lui Gauss
[ ][ ] [ ] [ ] [ ] [ ] A X B X A B − = ⇒ =
Metode iterative
- Metoda Jacobi
- Metoda Gauss-Seidel
- Metoda cu suprarelaxare succesivă (SOR)
Preview document
Conținut arhivă zip
- Metoda diferentelor finite.pdf
- Metoda elementelor finite.pdf
Alții au mai descărcat și
Întroducere Transformatorul electric este un aparat electromagnetic static funcţionînd pe baza inducţiei electromagnetice fiind destinat pentru...
1. Unitatea de masura pentru intensitatea campului electric (E) [..]....=..... (........ .... ..........) 2. Unitatea de masura pentru inductia...
Dipolul simetric se compune din douã conductoare simetrice situate de-a lungul unei axe la distantã relativ micã între ele (fig. 3.1). La capetele...
4.1. Antena canal de undã 4.1.1. Prezentarea antenei Datoritã avantajelor pe care le prezintã, antenele canal de undã au cãpãtat o largã...
Undele electromagnetice a cãror frecventa este cuprinsa între limitele 10-3 Hz si 1016 Hz se numesc unde radio. Aceste limite pot fi exprimate si...
INTRODUCERE ÎN COMUNICATII DE DATE: SCHEMA BLOC A SISTEMULUI DE COMUNICATII DE DATE, DESCRIERE, FUNCTIILE ELEMENTELOR, EXPLICAREA FUNCTIONARII PE...
Propagarea luminii în fibra optica Legile optice permit descrierea reflexiei totale la suprafata de separatie dintre miez-învelis a fibrei...
Reteaua în arbore (retea radiala) Centrele de comutatie C sunt interconectate într-un sistem arbore cu mai multe nivele (fig. 5.3.). Se observa...
Te-ar putea interesa și
INTRODUCERE Am ales să studiez comportamentul în regim dinamic al electromagnetului de curent continuu în mediul de simulare FLUX® deoarece...
Capitol I MODELE MATEMATICE DIFERENTIALE ALE CAMPULUI ELECTROMAGNETIC 1.1. MARIMI DE STARE ALE CAMPULUI ELECTROMAGNETIC În orice punct din...
Proiectarea şi monitorizarea proceselor de deformare plastică depinde de gradul de cunoaştere a caracteristicilor materialului de prelucrat,...
Capitolul 1. Clasificarea surselor de perturbaţii 1.1 Introducere Sursele de interferenţe electromagnetice pot fi de origine naturală (atmosferă,...
OBIECTUL METODEI ELEMEMNTELOR FINITE ÎN ANALIZA STRUCTURILOR MECANICE Calculul ingineresc, ca instrument ştiinţific pentru proiectarea,...
Curs 1. GIS este acronimul denumirii in limba engleza a Sistemelor Informatice Geografice: Geographic Information Systems (SUA), Geographies...
1. Noţiuni de teoria elasticităţii 1.1 Ecuaţii de bază În foarte multe domenii ale ştiinţei şi tehnicii, utilizarea unor instalaţii, utilaje şi...