Extras din curs

Rezumat

In aceasta treaba, o larga familie de LFSR- bazata pe generatori de secvente, asa numitul ceas-controlator de genaratoare in micsorare (CCSGs),a fost analizat si identificat cu un sub set de celule liniare automate (CA).De fapt , o pereche de modele liniare descriind comportamentul acestor CCSGs poate fi derivate.Algoritmul care converteste un CCSGs dat intr-o CA-baza lineara model, este foarte simplu si poate fi aplicat in sir unui CCSGs pentru un interes practic. Linearitatea asa ziselor modele celule poate fi folosita in mod avantajos in doua feluri:

- pentru analiza si/sau analiza codarii unui CCSGs

- pentru reconstruirea unor secvente de iesire obtinute de unele feluri de generatori

Introducere

Celulele automate (CA) sunt sisteme dinamice diferite caracterizate printr-o structura simpla dar un comportament complex [1-5] .Ele sunt construite din elemente individuale,numile celule, lega-te intre ele in multe feluri.CA au fost folosite in zone asa diferite ca simulatoarele fizice de sistem, procese biologice, evolutia unor specii, modele social-economice sau testarea modelelor de generatii.Ele sunt simple, modulare si structurile de cascada le fac foarte atractive pentru implementarile VLSI. CA pot fi caracterizate de mai multi parametrii de unde si comportamentul lor.Functia ¦ (asa numita regula) prin care celulele automate evolueaza la ur-matoarea stare, numarul celulelor vecine care se include in ¦, numarul de stari precedate incluse in ¦, structura geometrica si dimensiunea automatei (celulele pot fi aranjate intr-o linie sau intr-un patrat or cub impartit in 2, 3 sau mai multe dimensiuni), etc.

Pe de alta parte LFSR sunt dispozitive electronice folosite in secventele asa-zise obisnuite.Simplitatea crearii LFSR-urilor [6] , sunt usor de implementat si bunele lor proprietati statistice ale secventelor lor de iesire se transforma in blocuri naturale pentru designul genera-toarelor de secvente asa-zise obisnuite cu aplicatii in raspandirea comunicatiilor, testari de circuite, coduri de corectarea erorilor, simularile numerice sau scrierea secreta.

CA si LFSR sunt forme speciale a mai multor structuri de matematica generala: rangul masinilor finite [7] .In present CA cu o singura dimensiune a fost propusa ca o alternativa la LSFR [3,8-10] in sensul ca orice secventa generate de LSFR poate fi obtinuta dintr-o singura dimensiune a unui CA. Generatoarele de asa-zise secvente obisnuite implica mai multe LSFR-uri combinate cu ajutorul functiilor neliniare sau tehnici neregulate de pontare [11,12] . Atunci intrebarea care apare intr-un mod natural este: sunt oare CA uni-dimensionale in stare sa produca secvente obtinute cu LSFR? Raspunsul este da.Mai précis in aceast lucru este aratat ca o mare parte din LSFR-uri bazate pe generatoare neliniare asa numitele CCSG [13] , pot fi descrise in termenii unei configuratii de CA uni-dimensionala.Automata prezentata aici unifica intr-o simpla structura de generatoare de secvente(mentionata mai sus).Mai mult, CCSG-urile care sunt generatoare concepute si deghizate ca modele neliniare sunt convertite in CA-uri uni-dimensionale liniare. Odata ce generatorul a fost liniarizat tot backgroundul teoretic al al CA-ului liniar poate fi aplicat la analizarea lor sau/si la criptarea secreta.Procedura de conversie este foarte simpla si poate fi realizata in limita unui interes practice.

2.Structuri de baza

In subsectiunea urmatoare,introducem caracteristicile generale ale structurilor de baza cu care avem de-a face: CA uni-dimensionala, generatorul ce se micsoreaza si clasa de generatoare micsorate controlate prin ceas.Prin acest lucru doar CA binare si LSFR vor fi considerate.Mai mult, toate LSFR-urile cu care avem de-a face sunt LSFR-uri de lungime maxima ale caror secvente de iesire sunt secvenete PN [6] .

2.1.Celulele automate uni-dimensionale

CA uni-dimansioanle pot fi descrise ca n cellule inregistrate [1] , continutul acestor cellule este reinoit in acelas timp conform unei reguli particulare; aceasta este sa zicem o functie variabila k indicata de ¦.Daca fucntia ¦ este o functie liniara asa este si CA-ul.Cand k de intrare este considerate variabila binara, atuncieste un total de 2k diferite configuratii de vecini.Deci , pentru o CA cu continut binare pot fi pana la asezari diferite ale urmatorului rang.Mai mult, daca k=2r+1, atunci urmatorul rang xit+1 din celula xit de pinde de curentul rang al celulelor k vecine xit+1= ¦(xi-rt,…,xit,…,xi+rt) (i=1,…,n).

CA este numita uniforma daca toate celulele evolueaza sub aceeasi regula cat timp CA este numita hybrid daca diferite cellule evolueaza sub diferite reguli.La sfarsitul array-ului , doua diferite conditii limita sunt posibile: automata nula cand celula cu continut nul este alaturata celulelor extreme sau automata periodica cand celulele extreme sunt resupuse adiacente.

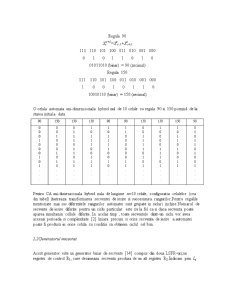
In acest articol, toate automatele considerate vor fi CA uni-dimensinale nule hibride cu k=3 si liniare regulile 90 si 150.Asemenea reguli sunt descrise cum urmeaza: