Extras din curs
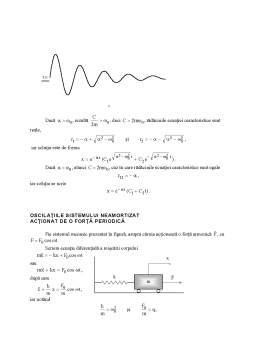
Când cele două oscilaţii perpendiculare au frecvenţe (pulsaţii) dife¬rite, adică (sau ), putând fi descrise de ecuaţiile
traiectoria a particulei supuse acţiunii simultane a celor două osci¬la¬ţii este o curbă relativ complicată, astfel de traiectorii purtând denumirea de figuri Lissajous.
Traiectoria va fi deci o curbă a cărei formă depinde de raportul celor două pulsaţii , precum şi de diferenţa de fază .
OSCILAŢII AMORTIZATE
Vom considera un sistem oscilator asupra căruia acţio¬nează forţa elastică şi o forţă de amortizare vâscoasă direct pro¬por¬ţio¬nală cu viteza corpului şi îndreptată în sens opus acesteia, în expresia sa, C purtând numele de coeficient de amortizare.
Pentru acest sistem, ecuaţia de mişcare se scrie sub forma
sau
în final, având
Efectuăm notaţiile
unde este pulsaţia proprie a sistemului, iar ecuaţia mişcării amortizate se scrie sub forma:
aceasta fiind o ecuaţie diferenţială omogenă, de ordinul al doilea, cu coefi¬cienţi constanţi, a cărei soluţie particulară este
şi deci
Substituind, vom obţine ecuaţia caracteristică
care admite soluţiile
Distingem următoarele cazuri:
a.) , rădăcini complexe: ;
b.) , rădăcini reale egale: ;
c.) , rădăcini reale distincte: .
Valoarea coeficientului de amortizare pentru care se numeşte coeficient de amortizare critică ,
de unde
Raportul adimensional va purta numele de factor de amor¬ti¬zare.
Considerăm cazul în care , efectuăm notaţia
rădăcinile ecuaţiei caracteristice fiind
iar soluţia generală a ecuaţiei diferenţiale va fi de forma
sau, prelucrând,
Cum amplitudinea mişcării este o funcţie de timp
putem scrie
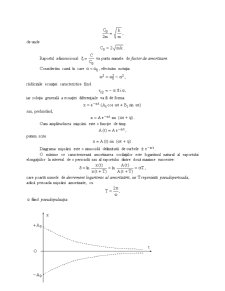
Diagrama mişcării este o sinusoidă delimitată de curbele .
O mărime ce caracterizează amortizarea oscilaţiilor este logaritmul natu¬ral al raportului elonga¬ţiilor la interval de o perioadă sau al raportului dintre două maxime succesive:
care poartă numele de decrement logaritmic al amortizării, iar T reprezintă pseudoperioada, adică perioada mişcării amortizate, cu
fiind pseudopulsaţia.
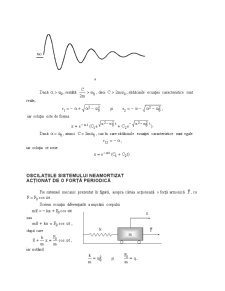
Dacă , rezultă , deci , rădăcinile ecuaţiei caracteristice sunt reale,
iar soluţia este de forma
Dacă , atunci , caz în care rădăcinile ecuaţiei carac¬te¬ristice sunt egale
iar soluţia se scrie
OSCILAŢIILE SISTEMULUI NEAMORTIZAT
ACŢIONAT DE O FORŢĂ PERIODICĂ
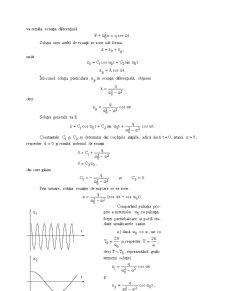
Fie sistemul mecanic prezentat în figură, asupra căruia acţio¬nează o forţă armonică , cu .
Scriem ecuaţia diferen¬ţială a mişcării corpului
sau
după care
iar notând
va rezulta ecuaţia diferenţială
Soluţia unei astfel de ecuaţii se scrie sub forma
unde
Înlocuind soluţia particulară în ecuaţia diferenţială, obţinem
Preview document
Conținut arhivă zip
- Compunerea a Doua Oscilatii Armonice Perpendiculare de Frecvente Diferite.doc