Cuprins
- I. RELAȚII DIN TEORIA ELASTICITĂȚII. RELAȚIILE DUHAMEL-NEWMANN 3
- II. SOLICITAREA AXIALĂ A BARELOR DREPTE . 6
- 2.1 BARA DE SECȚIUNE VARIABILĂ ÎNCĂLZITĂ LA TEMPERATURĂ
- CONSTANTĂ .. 6
- 2.2 BARĂ DE SECȚIUNE CONSTANTĂ CU VARIAȚIE DE TEMPERATURĂ ÎN
- LUNGUL EI . 7
- 2.3 SISTEME DE BARE ARTICULATE LA CAPETE 9
- III. ÎNCOVOIEREA BARELOR DREPTE .. 13
- IV. TENSIUNI TERMICE ÎN TUBUL CU PEREȚI GROȘI .. 13
- V. TENSIUNI TERMICE ÎN DISCURI ȘI CILINDRII . 18
- 5.2 TENSIUNI TERMOELASTICE ÎN DISCURI ... 18
- 5.2 CAZUL CILINDRILOR CONCENTRICI DIN MATERIALE DIFERITE .. 21
- VI. TENSIUNI TERMOELASTICE ÎN BARE FIXATE RIGID, UNIFORM ÎNCĂLZITE .. 23
- VII. TRANSFERUL DE CĂLDURĂ 26
- 7.1 TENSIUNI TERMOELASTICE ÎNTR-O PLACĂ CIRCULARĂ, LA CARE
- TEMPERATURA VARIAZĂ ÎN FUNCȚIE DE RAZĂ .. 26
- VIII. CALCULUL TENSIUNILOR TERMICE DIN PIESELE MOTORULUI CU ARDERE
- INTERNĂ .. 32
- 8.1 CALCULUL TENSIUNILOR TERMICE PENTRU CILINDRII MOTORULUI 32
- IX. Bibliografie .. 34
Extras din document
I. RELAȚII DIN TEORIA ELASTICITĂȚII. RELAȚIILE DUHAMELNEWMANN
Relații din teoria elasticității
În cazul materialelor izotrope și liniar elastice există trei constante elastice: E, G, υ. Relația dintre
cele trei constante de material este următoarea:
???? ????
????
2 ∙ ????1 ???? ????????
Legătura dintre tensorul tensiunilor și tensorul deformațiilor specifice este dată de legea
generalizată a lui Hooke:
Condiții la limită
Dacă se notează cu S’ suprafața laterală a unui corp, Sσ porțiunea de suprafață pe care sunt date
încărcările, Su porțiunea de suprafață pe care sunt cunoscute deplasările și px, py, pz componentele
încărcării exterioare, avem următoarele relații:
Relațiile Duhamel Newmann
Se consideră un paralelipiped infinit mic, dintr-un corp, așezat cu laturile paralele cu axele
sistemului și care este încălzit uniform cu:
Plecând de la legea generalizată a lui Hooke, se adaugă termenii αT și se obțin relațiile Duhamel-
Newmann:
Dialația sepcifică de volum:
???????? ???? ???????? ???? ???????? ???? ????????
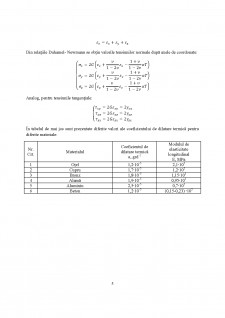
Din relațiile Duhamel- Newmann se obțin valorile tensiunilor normale după axele de coordonate:
Analog, pentru tensiunile tangențiale:
????
???????????? ???? 2???????????????? ???? 2????????????
???????????? ???? 2???????????????? ???? 2????????????
???????????? ???? 2???????????????? ???? 2????????????
În tabelul de mai jos sunt prezentate diferite valori ale coeficientului de dilatare termică pentru
diferite materiale:
Bibliografie
[1] Radeș M.,Tensiuni termice, Editura Printech, 2010
[2] . Elasticity Theory, Applications and Numerics, Sadd M., Elsevier Butterworth-Heinemann,
2005
[3] . Tripa P., Rezistența materialelor, Editura Mirton, 2001
[4] Mocanu D.R., Rezistența materialelor, Editura Tehnică, 1980
[5] Șerbu A., Dimitriu Șt., Rezistența Materialelor, Editura Universității Transilvania Brașov,
2005
[6] Ulea M. , Note de curs termoelasticitate
[4] http://www.mec.tuiasi.ro/RM2/capitole/Cap10.html
Preview document
Conținut arhivă zip
- Termoelasticitate.pdf
Alții au mai descărcat și
Definiţii, clasificări: Instalaţia electrică defineşte un ansamblu de echipamente electrice interconectate într-un spaţiu dat, formând un singur...
1. Elemente generale privind structura sistemelor hidropneumatice 1.1. Structura generală sistemelor hidropneumatice Funcția sistemului este de a...
Principiul întâi al termodinamicii în sisteme închise si deschise care au o evoluie între două stări oarecare; Principiul al doilea al...
Prepararea apei fierbinti se realizeaza utilizand agent termic primar abur saturat la 18 bar, in rezervoarele si schimbatorul de caldura. Initial...
Introducere in forajul sondelor 1.1 Notiuni introductive Sondele-sunt constructii miniere de forma cilindrica caracterizate printr-o lungime...
I. PREZENTAREA ȘI DESCRIEREA SISTEMULUI NAȚIONAL DE TRANSPORT GAZE NATURALE - SNTGN 1.1.CONSIDERAȚII GENERALE România dispune de zăcăminte de...
Te-ar putea interesa și
CAPITOLUL 1. INTRODUCERE, SCURT ISTORIC Acum mai bine de o sută de ani, JOHN WESLEY HYATT, cu brevetul de invenţie nr. 105336 din 12 iulie 1870...
INTRODUCERE PROTECTIA MEDIULUI Un mediu inconjurator sanatos reprezinta o conditie esentiala pentru proprietatea pe termen lung si pentru...
Progresul continuu al stiintei si al tehnicii a fost fara îndoiala, un rezultat firesc al cerintelor impuse de activitatile practice carora trebuia...
1. STADIUL ACTUAL AL CUNOŞTINŢELOR DIN DOMENIUL ALAMELOR ŞI BRONZURILOR 1.1Alamele 1. 1.1 Generalităţi, structură, proprietăţi Pentru...
Principii generale ale aliajelor cu memoria formei Aliajele cu memoria formei sunt componente metalice care pot memora o anumită formă impusă, iar...
1. NOTIUNI GENEREALE Fenomenul de „memorie a formei” este prezent la anumite aliaje cu transformare martensitică reversibilă în care martensita...
Abstract Aliajele cu memoria formei fac parte din grupa materialelor “inteligente” intermetalice, cu un conţinut de nichel (55 %) şi titan. Cele...