Optimizare

1. Formularea problemelor de optimizare

Din punct de vedere matematic problemele de optimizare se pot pune sub forma:

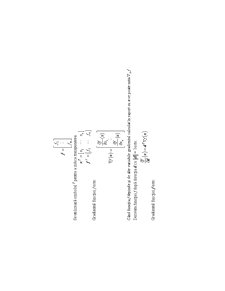
Fie data o functie . Sa se determine fDRRn:⊂→x* si astfel incat (ffx*=()()ffxxDfx**min==∈

Functiase numeste funcţie obiectiv, iar prin “optimizarea lui ” se intelege determinarea lui ffx* si a lui . Domeniul de calcul este definit de obicei astfel: f*D

()(){}DxRcximcximmnii=∈==′≥=′+0101,,.,;,,.,

unde functiile se numesc functii restrictii. cRRimin:,,.→=1

Problema de optimizare poate fi pusă si in forma standard a unei probleme de minimizare cu restricţii neliniare astfel:

()()(){}min,,.,;,,.,fxcximcximmii==′≥=′+0101

O problemă de maximizare se poate pune imediat în această formă standard prin schimbarea semnului funcţiei obiectiv. Adică o problemă de forma:

()maxxDgx∈

se scrie sub forma standard punând:

()()fxgx=−

2. Clasificarea problemelor de optimizare

Pentru clasificarea problemelor de optimizare se pot avea în vedere mai multe aspecte:

a) Evidenţierea unor proprietăţi speciale ale problemei, care pot duce la creşterea eficienţei metodelor de rezolvare.

Proprietăţi pentru funcţia obiectiv f(x):

- funcţie de o variabilă;

- funcţie liniară;

- funcţie sumă de pătrate de funcţii liniare;

- funcţie pătratică;

- funcţie sumă de pătrate de funcţii neliniare;

- funcţie neliniară diferenţiabilă;

- funcţie neliniară nediferenţiabilă;

Proprietăţi pentru funcţiile restricţii ci(x):

- nu există restricţii;

- restricţii margini simple pentru variabile;

- funcţii liniare;

- funcţii neliniare diferenţiabile;

- funcţii neliniare nediferenţiabile;

Corespunzător acestor proprietăţi există de exemplu:

- probleme de optimizare liniare (cu funcţia obiectiv şi restricţiile liniare);

- probleme de optimizare pătratică (cu funcţia obiectiv pătratică şi restricţiile liniare);

- probleme de optimizare fără restricţii;

- probleme de optimizare cu restricţii liniare;

- probleme de optimizare cu restricţii neliniare;

b) Dimensiunea problemelor.

Dimensiunea problemelor este dată de numărul de variabile şi de numărul de restricţii. Au fost rezolvate probleme având dimensiunea de ordinul 106 dar de complexitate redusă (probleme de programare liniară de structură specială) şi probleme având dimensiunea de ordinul 102 dar de complexitate ridicată (probleme generale de programare neliniară).

- cazul unei singure variabile se tratează întotdeauna ca un caz special;

- problemele de mici dimensiuni sunt problemele ale căror date pot fi reţinute în memoria internă a calculatorului;

- problemele de mari dimensiuni sunt problemele ale căror date nu se pot reţine în memoria internă a calculatorului pe care se rezolvă problema.

c) Informaţia disponibilă algoritmului de rezolvare pe durata calculelor.

- se pot cunoaşte valorile funcţiilor;

- se pot cunoaşte valorile funcţiilor şi valorile derivatelor de ordinul I;

- se pot cunoaşte valorile funcţiilor, valorile derivatelor de ordinul I şi valorile derivatelor de ordinul II;

d) Complexitatea problemelor.