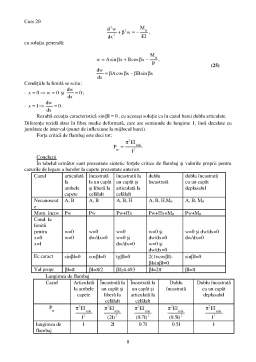
Extras din curs
INTRODUCERE
1. Obiectul Rezistentei materialelor si locul acesteia în
ansamblul disciplinelor ingineresti. Scurt istoric.
În practica de toate zilele, inginerului i se pune în permanenta problema alegerii materialului,
formei si dimensiunilor unor corpuri, astfel încât acestea sa nu atinga stadiul de cedare sau
modificare excesiva a geometriei lor initiale, sa prezinte siguranta în raport cu pragul de aparitie a
acestor fenomene în decursul exploatarii si, în acelasi timp, sa satisfaca aceste cerinte în mod cât
mai economic. Principiile care stau la baza rezolvarii rationale a acestor probleme constituie
obiectul Rezistentei materialelor. Scopul acestei discipline este studiul comportarii elementelor de
constructii sau de masini sub actiunea altor corpuri si, pe baza concluziilor acestui studiu, stabilirea
relatiilor cantitative, matematice, care asigura în conditii de economicitate rezistenta, rigiditatea si
stabilitatea constructiilor sau a ansamblurilor de masin1.
Rezistenta materialelor face parte din grupul de discipline numit Mecanica constructiilor sau,
mai extins, Mecanica corpului deformabil, grup care include: Rezistenta materialelor, Teoria
elasticitatii, Teoria plasticitatii, Statica, dinamica si stabilitatea constructiilor, Mecanica
pamânturilor, etc.
Interactiunea dintre corpuri fiind reprezentata obisnuit prin forte, se vor folosi curent în
rezolvarea problemelor cunostinte din Mecanica teoretica. Spre deosebire însa de Mecanica
teoretica, care admite modelul corpului rigid, nedeformabil, Rezistenta materialelor care studiaza
efectul fortelor (numite încarcari sau sarcini) pe si mai ales în interiorul elementelor, nu poate face
abstractie de proprietatea de deformabilitate a corpurilor. Din acest motiv în Rezistenta materialelor
se admite modelul corpului deformabil a carui configuratie geometrica se modifica sub actiuni
exterioare. Modificarile geometrice au drept consecinta aparitia unor forte interioare între particulele
materialelor care alcatuiesc corpul.
De asemenea fortele pot sa varieze în timp, în acest caz solicitarea este dinamica, sau pot varia
ca intensitate cu o viteza foarte mica, de la 0 la o valoare finala, care ramîne constanta, solicitarea
fiind statica.
Ipotezele principale ce se fac asupra solidului deformabil sunt:
1. Mediul din care este alcatuit solidul deformabil este continuu. Aceasta înseamna ca orice
domeniu oricât de mic (infinitezimal) din corp contine materie, permitând utilizarea aparatului
analizei matematice clasice, considerarea tuturor marimilor care apar, tensiuni, deformatii, deplasari
ca functii de punct. Aceasta presupunere se justifica prin dimensiunile foarte mici pe care le au
particulele din care este alcatuit mediul fata de dimensiunile corpurilor studiate.
2. Mediul este omogen adica are aceleasi proprietati în toate punctele sale. Aceata ipoteza, se
va vedea, nu este întotdeauna îndeplinita, fiind posibila în unele cazuri considerarea
neomogeneitati1.
3. Mediul este izotrop, adica are aceleasi proprietati pe toate directiile sale.
4. Deplasarile punctelor solidului datorita deformabilitatii acestuia sunt forte mici în
comparatie cu dimensiunile acestuia. Aceasta conduce la relatii liniare între deformatii si derivatele
partiale ale componentelor deplasari1. Aceasta ipoteza, conduce la asa numitul calcul de ordinul
întâi, în care fortele interioare se vor calcula din ecuatii de echilibru (prin metoda sectiunilor),
considerând punctele de aplicatie ale fortelor în pozitia initiala, când corpul nu era deformat. În
unele cazuri este necesar sa nu fie luata în consideratie, efectuându-se calcule de ordinul do1.
5. Mediul este liniar elastic. Aceasta înseamna ca relatia între tensiuni si deformatii este o
relatie biunivoca liniara. Aceasta ipoteza implica caracterul reversibil al deformatiei si corespunde
întelegerii curente a corpului elastic, care revine la starea sa initiala odata cu anularea sarcinilor
care l-au solicitat.
2. Elemente fundamentale în definirea modelului corpului deformabil.
Schematizând proprietatile materiei, adoptând ipoteze referitoare la cauzele, desfasurarea si
efectele unor fenomene reale în scopul elaborarii unei teorii, Rezistenta materialelor, în studiu,
înlocuieste modelul fizic real printr-un model ipotetic, de calcul.
2.1 Modelarea materiei si a geometriei corpurilor.
Rezistenta materialelor face abstractie de structura discreta (atomica) a materiei, presupunândo
continua. Prin continuum material se întelege un corp al carui volum este umplut complet cu
substanta. Drept consecinta a acestei ipoteze, fiecarui punct din corp i se pot atasa marimi fizice
reprezentate prin functii continue de coordonatele punctulu1.
Se poate considera ca materia este omogena, adica proprietatile ei nu se modifica de la punct
la punct. Majoritatea materialelor sunt izotrope, adica proprietatile sunt aceleasi pe directii diferite
de studiu. Corpurile care intra în componenta utilajelor si masinilor numite obisnuit elemente de
constructii sau organe de masini sunt portiuni de continuum delimitate spatial. Reprezentarea
corpurilor în spatiu se face într-un sistem de referinta cartezian.
Dupa raportul dintre principalele dimensiuni corpurile pot fi împartite în:
- Bare. Sunt acele corpuri la care o dimensiune (lungimea) este mult mai mare
decât celelalte doua. Elementele caracteristice a unei bare sunt forma si dimensiunile sectiunii
transversale normale pe axa bare1.
Prin sectiune normala într-un punct pe lungimea barei se întelege sectiunea de arie minima
obtinuta prin intersectia acesteia cu un plan; axa barei reprezinta curba data de succesiunea centrelor
de greutate ale sectiunilor normale. Dupa forma axei longitudinale barele pot fi: drepte, curbe plane
sau curbe spatiale (figura 1). Dupa forma sectiunii transversale barele pot fi: cu sectiune transversala
deschisa si închisa.
Daca sectiunile transversale ale barelor sunt de dimensiuni neglijabile ele se numesc fire sau
cabluri.
Fig. 1
- Placi. Sunt acele corpuri la care doua dimensiuni (lungimea si latimea) sunt mari în raport cu
a treia dimensiune.
Locul geometric al mijloacelor grosimilor placii se numeste suprafata mediana, grosimea
placii fiind masurata normal pe suprafata mediana. Dupa forma suprafetei mediene placile pot fi:
placi plane, placi cu simpla curbura, placi cu dubla curbura (figura 2). Grosimea placii este cel mai
des constanta. Când placa are grosime mica, putându-se neglija rigiditatea dupa grosime ea se
numeste membrana.
Preview document
Conținut arhivă zip
- Curs_1.pdf
- Curs_10.pdf
- Curs_11.pdf
- Curs_12.pdf
- Curs_13.pdf
- Curs_14.pdf
- Curs_15.pdf
- Curs_16.pdf
- Curs_17.pdf
- Curs_18.pdf
- Curs_19.pdf
- Curs_2.pdf
- Curs_20.pdf
- Curs_21.pdf
- Curs_22.pdf
- Curs_23.pdf
- Curs_24.pdf
- Curs_25.pdf
- Curs_26.pdf
- Curs_27.pdf
- Curs_28.pdf
- Curs_29.pdf
- Curs_3.pdf
- Curs_4.pdf
- Curs_5.pdf
- Curs_6.pdf
- Curs_7.pdf
- Curs_8.pdf
- Curs_9.pdf