Cursuri Econometrie

Teoria

economică

Matematica

deterministă

Teoria

probabilităţilor

Economia

matematică

Statistica

matematică

Econometria

1 PRELIMINARII CONCEPTUALE ŞI MATEMATICE

1.1 Obiectul, structura, etapele şi ramurile econometriei

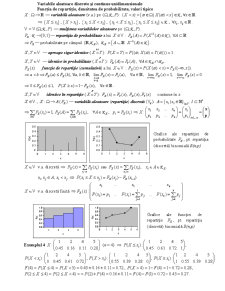
Econometria clasică — aplicare a teoriei economice, a matematicii şi a tehnicilor statisticii matematice la verificarea ipotezelor, estimarea şi predicţia fenomenelor economice. Teoria economică propune modele ale realităţii, matematica le formulează în termeni de funcţii deterministe, iar statistica evaluează parametrii aleatori ai respectivelor funcţii.

Societatea de econometrie (Econometric Society)— înfiinţată în Anglia (1930), cu revista Econometrica (1933): cele 3 componente ale econometriei sunt necesare, dar nu suficiente; doar sinteza lor specifică îi defineşte domeniul şi metodele. Economia matematică clasică — cu modelele deterministe. Neglijarea unor factori cere introducerea unor componente stohastice, sub forma unor perturbaţii/erori aleatoare. Factorii aleatori: — multitudinea factorilor ce influenţează fenomenele economice, — incertitudinile comportamentului uman. Economia matematică contemporană (cu modele economice sub formă de funcţii stohastice) — bazată pe teoria economică, matematica deterministă şi teoria probabilităţilor. Economia matematică şi statistica matematică — folosite direct de către econometrie. Studiul evenimentelor asociate experimentelor aleatoare şi al mărimilor legate de acestea — domeniul teoriei probabilităţilor şi al statisticii matematice. Teoria probabilităţilor — experimentele aleatoare ideale, modele abstracte ale celor reale. Statistica matematică — compararea modelelor ideale cu fenomenele reale (pt. particularizarea modelelor reale şi descoperirea cauzelor neconcordanţelor). Econometria contemporană — studiul sistematic al fenomenelor economice, folosind datele observate. Tehnicile econometrice — 2 categorii principale: a) tehnici de regresie (pentru găsirea funcţiilor ce exprimă dependenţele între variabilele modelului); b) tehnici de analiză a seriilor temporale (pt. clarificarea structurii lor, prin netezirea acestora sau prin descompunerea în componentele lor principale — tendinţă, ciclicitate, sezonalitate şi eroare). Regresia — abordare explicativă (eventual cauzală) a fenomenului („de ce?”). Seriile temporale —abordare comportamentistă („fenomenologică”) („cum?”).

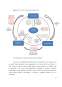
Metodologia studiilor econometrice clasice — 4 etape:

1) construcţia modelului teoretic matematic al fenomenului economic studiat (cu metodele economiei matematice: dependenţe funcţionale între variabilele modelului + constante necunoscute — parametri);

2) construcţia modelului econometric (specificarea modelului teoretic: funcţii stohastice explicite + caracteristicile teoretice a priori asupra mărimilor parametrilor funcţiei);

3) colectarea datelor asupra variabilelor modelului, estimarea parametrilor şi validarea semnificaţiei acestora (prin tehnicile statisticii matematice);

4) dacă modelul este invalidat, se trece la revizuirea lui (prin întoarcerea la una din etapele precedente);

altfel: — se poate căuta un model şi mai adecvat, sau

— se foloseşte modelul existent la diverse predicţii şi la evaluarea politicilor economice.

Modelele deterministe — invalidate printr-un singur exemplu negativ.

Modelele stohastice: — invalidate prin atingerea anumitei ponderi (discutabile) a exemplelor negative;

— mai puţin precise decât cele deterministe, dar mai „robuste”.

Econometria: - teoretică — tehnici şi metode generale, condiţii de aplicare, consecinţele nesatisfacerii;

- aplicată — aplicarea econometriei teoretice în diverse domenii (cu date reale sau simulate).

Econometria: - micro-econometrie (pt. fenomene microeconomice)

- macro-econometrie (pt. fenomene macroeconomice).

Construcţia

modelului

matematic

Construcţia

modelului

econometric

Estimarea şi

validarea

modelului

Date

statistice

Predicţie

şi evaluarea politicilor

Revizuire

1.1.1 Experimente aleatoare spaţii de eşantionare şi probabilităţi „naive”

Experimentele aleatoare — experimente legate de condiţii întâmplătoare şi despre ale căror rezultate nu

se poate spune cu certitudine dacă s-au produs sau nu, decât după ce s-au produs („aleator”= „stohastic”).

Populaţie — mulţime de elemente (indivizi) cu diverse caracteristici..

Exemple: a) mulţimea celor două feţe ale unei monede (notate cu S pentru stemă şi V pentru valoare), 2)

feţele unui zar (cu 1-6 puncte), 3)o mulţime de bile (cu caracteristici de sfericitate, greutate şi culoare), 4) cele

52 de cărţi de joc diferite dintr-un pachet; 5) angajaţii unei întreprinderi, 6) populaţia umană a unei ţări.

Populaţia poate conţine diverse submulţimi (colective), cu valori deosebite ale unei caracteristici.

Exemple: 1) la un zar — feţele cu număr par şi cele cu număr impar de puncte, 2) la bile — cele de

culoare albă şi cele negre, 3) la cărţile de joc — cele de treflă, de cupă, de carou şi de pică.

Submulţimile — structurare caracterizabilă numeric (şi, eventual, grafic) a mulţimii (populaţiei) iniţiale.

Structurarea — prin numărare (pt. submulţimile discrete),

— prin măsurare (pt. submulţimile continue).

Eşantioane — submulţimi obţinute prin alegeri (sau selectări) întâmplătoare (prin moduri care să

păstreze, pe cât posibil, structura populaţiei iniţiale). De obicei, se presupune că orice element din populaţie are

şanse egale cu ceilalţi de a fi ales.

Exemple 1) aruncarea banului sau a zarului —să nu se poată determina dinainte căderea pe o anumită

faţă, 2) extragerea unor bile dintr-o urnă — amestecate în prealabil (ca la loterii).

Regulile de extragere (sau de alegere) a elementelor eşantionului trebuie să fie precizate; există şi

condiţii implicite, care este bine să fie explicitate.

Exemple: 1) despre monede sau zaruri se presupune că au densităţi omogene, 2) despre bile — că sunt

de mărimi şi greutăţi egale, 3) despre cărţi — că au aceeaşi formă şi mărime.

Extragerile pot fi efectuate în diverse moduri de oameni, sau se pot produce prin anumite fenomene

naturale sau sociale, pe care oamenii doar le observă şi le analizează.

Experimentele — pot fi imaginare (cu obiecte şi condiţii ideale, neglijând condiţiile neesenţiale).

— încep prin precizarea spaţiului tuturor evenimentelor posibile (spaţiul de eşantionare)

Exemplu: la aruncarea cu moneda sau cu zarul, se neglijează posibilitatea căderii pe muchie, respectiv

pe colţ; spaţiul de eşantionare pentru două aruncări cu un ban având feţele cu stemă (S) sau valoare (V) —

mulţimea {SS, SV, VS, VV} a perechilor de rezultate posibile.

Abstracţia permite să înlocuim un experiment aleator cu altul mai uşor de executat, cu aceleaşi rezultate.

Experimentele cu extrageri de bile din una sau mai multe urne pot servi ca model pentru orice spaţiu de

eşantionare cel mult numărabil.

Exemplu: aruncarea cu banul poate fi înlocuită prin extragerea unei bile dintr-o urnă cu două bile de

culori diferite, urmată de punerea la loc (înlocuirea) celei extrase, înaintea unei noi extrageri.

Evenimente aleatoare: — rezultatele unui experiment aleator;

— elementare (nu pot fi descompuse în elemente mai simple) sau

— compuse (pot fi descrise prin asocierea unor evenimente elementare).