Estimating force requirements for crisis response operations

Abstract

Similar to emergency and rescue operations, Crisis Response Operations (CRO) are triggered by events which occur repeatedly at irregular intervals. However, in contrast to the former they typically last for extended time periods thus requiring regular rotation of the forces involved. Since both inter-arrival times and duration of CRO can be described in terms of probability functions, various stochastic simulation models have been developed to generate, through a series of simulation experiments, the data base required for estimating so-called mission stacks and force requirements for CRO. However, based on experiments using the simulation model STORM (Stochastic Requirements Model) it was found that a data base sufficient for force planning purposes requires an excessive number of experiments. Therefore, as the structure of STORM corresponds to what is known in telecommunication systems analysis as a multiple service multiple resource loss network (MSMR), albeit without rotational service, the authors extend the analytical methods used in telecommunication analysis and develop a technique for approximating blocking probabilities that account for different rotational service strategies.

1. Introduction

Historical evidence indicates that, similar to emergency and rescue operations, Crisis Response Operations (CRO) are triggered by events which occur repeatedly at irregular intervals. However, in contrast to the former they typically last for extended time periods thus requiring regular rotation of the forces involved. When analyzing the data on operations-other-than-war (OOTW) compiled by John Sherwood (1995) it was discovered that their inter arrival time as well as their duration can be described in terms of exponential probability distribution functions. Therefore, Cherry/Huber/Hodgson (1998) suggested that queuing theory models might be used to analyze CRO requirements. They illustrated the idea by modeling the process of allocating units to CRO in form of a simple M/M/n queuing system having the capacity of handling up to a given number of CRO of one type simultaneously. Subsequently, this initial prototype simulation model was enriched and became known as the Stochastic Requirements Model (STORM) which was used by Huber and Cherry (1998) to investigate the relation between readiness and unit rotation policy and by Huber and Schäfer (2002) for analyzing German Army structural bottlenecks in CRO similar to SFOR and KFOR.1

1 It should be pointed out, however, that the first applications-oriented analysis applying queuing theory in support of force planning was done under the acronym SADE at the US Army’s Concepts Analysis Agency (CAA) by Patrick DuBois (1998) who developed a simulation model for generating, based on historical data such as those compiled by Sherwood, so-called simultaneity stacks for small scale contingencies (SSC) as a basis for predicting likelihood of concurrent SSC operations in the period of 1998 and 2006. STORM can be considered an extension of the SADE

The study experience with STORM revealed, however, that an excessive number of simulation experiments was required to generate a data base sufficient for force planning purposes in particular with regard to accounting for readiness requirements and mission priorities. Therefore, the development of analytic approximation methods permitting straightforward computation of force requirements as a function of readiness or availability specifications became the focus of a research project reported in this paper. Since the quality of the analytic methods is assessed in terms of how well they approximate the results obtained from simulation experiments, a review of the essential characteristics of STORM is given first. A detailed description of the model is provided by Schäfer (2003).

2. The Stochastic Requirements Model (STORM)

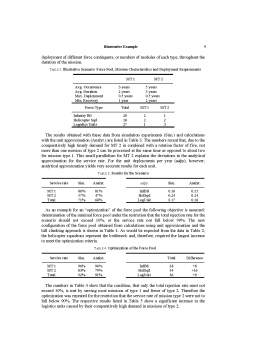
STORM performs a discrete event simulation over a time period that is long enough so that a stationary phase is reached when the variables of interest assume stable values. The input data fall into two categories:

- the force pool, comprising different types (j = 1, .m) and numbers bj of force modules from which CRO task forces are compiled, denoted by the vector b = (b1, .bm);

- the set of different mission types (i = 1, .n) each specified by their expected occurrence per time unit (arrival rate λi), expected duration Ti or service rate μi, the types and numbers of force modules required [aij] (with 0 ≤ aij ≤ bj), and the rotation policy. Both arrival rate and duration of missions are stochastic variables determined by specific probability distributions (e.g. exponential distribution) and their parameters.

Rotation is necessary because in most cases the duration of a mission will exceed the maximum acceptable deployment time of an individual force unit or module. In STORM the rotation policy is defined by the tuple (TD, TR). TD specifies the maximum time of continuous deployment after which the forces have to be replaced, directly followed by the minimum recovery time TR indicating the time after which the respective unit or module is available for the next deployment at the earliest. The resultant rotation process is illustrated by Figure 1.