Circuite logice combinaționale elementare

1. OBIECTUL APLICATIEI

Aplicatia are ca scop familiarizarea cu portile logice NU, SI, SAU, SI-NU, SAU-NU si SAU-EXCLUSIV, care fac parte din clasa circuitelor logice combinationale. Se prezinta teoretic principiile si legile algebrei booleene, simbolurile portilor logice, functiile logice pe care acestea le realizeaza si tabelele de adevar corespunzatoare. Se verifica practic cu voltmetrul electronic pe macheta de laborator tabelele de adevar ale portilor logice studiate si se ridica caracteristica de transfer a portii logice NU. Se analizeaza portile logice prin simulare PSpice pe baza formelor de unda ale semnalelor de iesire cand la intrare se aplica un semnal (semnale) logice avand o succesiune oarecare de valori logice.

2. INTRODUCERE TEORETICA

Circuitele logice sunt circuite electronice care opereaza cu semnale logice (digitale) care nu pot lua decat doua valori (niveluri) logice:

• Nivelul logic 0: semnifica, de exemplu, lipsa semnalului (0V);

• Nivelul logic 1: semnifica, de exemplu, prezenta semnalului (5V).

De aceea, forma de unda a semnalelor logice este intotdeauna dreptunghiulara. De exemplu in figura 1 succesiunea de valori logice ale tensiunii V(1) este 10101.

1

1 1

0 0

0s 1s 2s 3s 4s 5s

Fig. 1 Exemplu de semnal logic

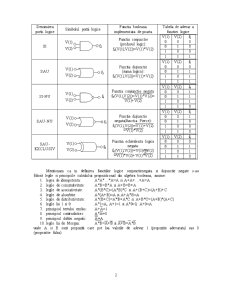
In tabelul 1 se prezinta simbolul, functia logica implementata (denumire, relatie booleana si eventuale forme echivalente) si tabela de adevar pentru portile logice elementare NU, SI, SAU, SI-NU, SAU-NU si SAU-EXCLUSIV care prelucreaza semnalele logice V(1) sau/si V(2).

Tabelul 1:

Denumirea

portii logice Simbolul portii logice Functia booleana implementata de poarta Tabela de adevar a functiei logice

NU

Functia negatie:

f1(V(1))=V(1) V(1) f1

0 1

1 0

Denumirea

portii logice Simbolul portii logice Functia booleana implementata de poarta Tabela de adevar a functiei logice

SI

Functia conjunctie (produsul logic):

f2(V(1),V(2))=V(1)*V(2) V(1) V(2) f2

0 0 0

0 1 0

1 0 0

1 1 1

SAU

Functia disjunctie (suma logica): f3(V(1),V(2))=V(1)+V(2) V(1) V(2) f3

0 0 0

0 1 1

1 0 1

1 1 1

SI-NU

Functia conjunctie negata: f4(V(1),V(2))=V(1)*V(2)= V(1)+V(2) V(1) V(2) f4

0 0 1

0 1 1

1 0 1

1 1 0

SAU-NU

Functia disjunctie negata(functia Pierce): f5(V(1),V(2))=V(1)+V(2) =V(1)*V(2) V(1) V(2) f5

0 0 1

0 1 0

1 0 0

1 1 0

SAU-EXCLUSIV

Functia echivalenta logica negata: f6(V(1),V(2))=V(1)OV(2) =V(1)*V(2)+V(1)*V(2) V(1) V(2) f6

0 0 0

0 1 1

1 0 1

1 1 0

Mentionam ca in definirea functiilor logice conjunctienegata si disjunctie negate s-au folosit legile si principiile calculului propozitional din algebra booleana, anume:

1. legea de idempotenta: A*A*…*A=A si A+A+…+A=A

2. legile de comutativitate: A*B=B*A si A+B=B+A

3. legile de asociativitate: A*(B*C)=(A*B)*C si A+(B+C)=(A+B)+C

4. legile de absorbtie: A*(A+B)=A si A+A*B=A

5. legile de distributivitate: A*(B+C)=A*B+A*C si A+B*C=(A+B)*(A+C)

6. legile lui 1 si 0: A*1=A, A+1=1 si A*0=0, A+0=A

7. principiul tertului exclus: A+A=1

8. principiul contradictiei: A*A=0

9. principiul dublei negatii: A=A

10. legile lui de Morgan: A*B=A+B si A+B=A*B

unde A si B sunt propozitii care pot lua valorile de adevar 1 (propozitie adevarata) sau 0 (propozitie falsa).