Cuprins
- TEORIA ERORILOR DE MĂSURĂ
- MĂSURARE, SISTEMUL INTERNAŢIONAL, ANALIZĂ DIMENSIONALĂ
- UNITĂŢI DE MĂSURĂ, TRANSFORMĂRI DE UNITĂŢI DE MĂSURĂ
- STUDIUL GOLIRII UNUI REZERVOR CU LICHID
- ETALONAREA UNUI GENERATOR DE OSCILAŢII ELECTRICE UTILIZÂND METODA FIGURILOR LISSAJOUS
- DETERMINAREA VITEZEI DE PROPAGARE A SUNETELOR PRIN AER UTILIZÂND TUBUL KÖNIG
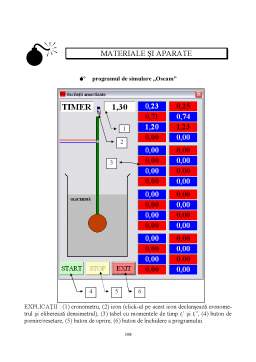
- OSCILATORUL AMORTIZAT
- VITEZA DE PROPAGARE A ULTRASUNETELOR ÎNTR-UN LICHID
- MĂSURAREA NIVELULUI DE POLUARE SONORĂ
- ETALONAREA REŢELELOR DE DIFRACŢIE CU RADIAŢIE LASER MONOCROMATICĂ
Extras din laborator
TEORIA ERORILOR DE MĂSURĂ
Măsurare
Erori sistematice
Erori întâmplătoare
Valoarea medie, abaterea pă-tratică medie
Erori absolute, erori relative
Măsurare indirectă, eroarea unei măsurări indirecte
Măsurarea mărimilor fizice este acti-vitatea principală în orice experienţă de laborator, dar nu numai în asemenea si-tuaţii (gândiţi-vă, de exemplu, la măsu-rarea gradului de poluare a aerului pe o arteră de circulaţie cu trafic intens). Gradul de încredere în valorile măsurate este strâns legat de corectitudinea cu ca-re au fost făcute măsurătorile şi de ero-rile care puteau interveni. De aceea, este necesară stabilirea unor reguli stricte privind modul de efectuare a măsurăto-rilor şi stabilirea gradului de eroare a acestora. Aplicaţia de faţă urmăreşte să vă familiarizeze cu aceste reguli.
CUVINTE CHEIE
TEMA APLICAŢIEI
SCOPUL APLICAŢIEI
Cunoaşterea tipurilor de erori de măsură. Cunoaşterea modului de calcul al erorilor în măsurătorile directe şi indirecte.
DEFINIŢII ŞI FORMULE
Măsurarea unei mărimi fizice înseamnă a determina de câte ori se cuprinde în ea o mărime fizică de acelaşi fel, aleasă ca unitate de măsură. Măsurarea poate fi directă sau indirectă. De exemplu, distanţa dintre două obiecte ar putea fi măsu-rată în mod direct cu rigla, dar ar putea fi determinată şi indirect cunoscând vite-za luminii şi măsurând timpul în care o rază de lumină parcurge distanţa dintre ele. În funcţie de cazul concret se alege una dintre cele două metode de măsură.
Operaţia de măsurare este însoţită de erori. Erorile de măsură pot fi împărţite în două categorii: sistematice şi întâmplătoare.
Erorile sistematice pot avea la origine mai multe cauze : defectele aparatelor de măsură (de exemplu, ora afişată de un ceas care nu merge exact), utilizarea unui principiu de măsură greşit (de exemplu, aprecierea cantităţii de lichid dintr-un vas tronconic pe baza înălţimii acestuia) sau greşelilor făcute de observator (de exemplu, plasarea sa incorectă faţă de aparatul de măsură, ceea ce conduce la ci-tirea incorectă a indicaţiilor aparatului). Aceste erori pot fi înlăturate doar prin repararea aparatului defect, regândirea principiului măsurătorii sau înlăturarea greşelilor de observare.
Erorile întâmplătoare se datorează în special lipsei de precizie a citirilor indi-caţiilor instrumentelor de măsură şi constituie un factor legat exclusiv de per-soana experimentatorului. În acest cazuri, rezultatul unei măsurători este fie mai mare, fie mai mic în comparaţie cu valoarea corectă. Caracterul statistic al ero-rilor întâmplătoare face ca la repetarea de un mare număr de ori a determinărilor numărul valorilor mai mari decât cele reale să egaleze practic numărul valorilor mai mici. Rezultă de aici că erorile întâmplătoare pot fi compensate prin repe-tarea de un mare număr de ori a determinărilor şi medierea rezultatelor obţinute. Printre erorile întâmplătoare întâlnim şi erorile grosolane, care se pot distinge de celelalte prin aceea că oferă valori complet diferite de şirul celorlalte valori experimentale. Erorile grosolane sunt înlăturate prin refacerea măsurătorii sau ignorarea rezultatului aberant.
Valoarea medie. Inerent, la măsurarea directă a oricărei mărimi fizice se face o eroare de măsură. Repetând determinările de un număr mare de ori, rezultatele se distribuie simetric în jurul valorii adevărate. De aceea, prin medierea aritmeti-că a datelor obţinute, mai ales dacă numărul determinărilor este foarte mare,
există posibilitatea ca erorile care supraestimează valoarea adevărată să se com-penseze cu acelea care o subestimează. Acesta este motivul pentru care, în urma şirului de măsurători, valoarea acceptată ca rezultat final este media aritmetică a rezultatelor tuturor măsurătorilor, adică valoarea medie.
Abaterea pătratică medie. Faptul că valoarea medie aproximează cel mai bine valoarea adevărată a mărimii fizice pe care o măsurăm, nu înseamnă că ştim şi cât de siguri putem fi de precizia măsurătorii. Precizia este legată de intervalul dintre cea mai mică valoarea obţinută prin măsurare şi cea mai mare valoare. Cu cât acest interval este mai mare în comparaţie cu valoarea medie a mărimii mă-surate, cu atât precizia măsurătorii este mai mică şi încrederea în privinţa rezul-tatului obţinut este ea mai mică. Imaginaţi-vă că aţi da examen din aceeaşi mate-rie cu 10 profesori diferiţi. Dacă la toate examenele aţi obţine note între 5 şi 7, aţi putea fi destul de siguri că ştiţi de nota 6. Dar dacă gama notelor obţinute ar fi între 2 şi 10, media fiind tot 6, aţi mai avea siguranţa că aţi fost examinat co-rect ? De aceea, alături de valoarea medie, trebuie prezentată şi o valoare care să exprime precizia măsurătorii. În cale mai multe cazuri această valoare comple-mentară este abaterea pătratică medie, a cărei formulă şi a cărei semnificaţie vă vor fi prezentate în paginile următoare.
Eroarea absolută reprezintă intervalul în care este cel mai probabil să se afle valoarea mărimii măsurate. Eroarea relativă este raportul dintre eroarea absolu-tă şi valoarea medie a mărimii măsurate. De exemplu, dacă cumpăraţi o pungă de zahăr pe care scrie „Gramaj : 1000 g ± 10 g” eroarea absolută de măsură este de 10 g, iar cea relativă de 1%.
Măsurarea indirectă a unei mărimi fizice se face atunci când nu este posibilă măsurarea ei directă. Se utilizează o lege a fizicii care cuprinde atât mărimea fi-zică pe care dorim s-o măsurăm indirect, cât şi alte mărimi fizice a căror măsura-re directă este posibilă. Valoarea pe care o căutăm se exprimă în virtutea legii folosite, în funcţie de valorile măsurate ale celorlalte mărimi fizice. Eroarea fina-lă de măsurare este determinată cunoscând erorile făcute la măsurarea fiecăreia dintre mărimile fizice implicate.
ASPECTE TEORETICE
Teoria erorilor întâmplătoare
Să presupunem că trebuie măsurată o mărime fizică oarecare X. Pentru aceasta se face un şir de determinări care generează valorile : x1, x2,… xN. Aceste valori diferă între ele şi este puţin probabil ca măcar una dintre ele să reprezinte valoarea exactă a mărimii căutate.
Când toate măsurătorile au fost efectuate în aceleaşi condiţii de precizie experimentală se poate presupune că abaterile ξk = (xk - X) sunt distribuite sta-tistic în jurul lui zero. Dacă numărul determinărilor este foarte mare, N >> 1, atunci probabilitatea de apariţie a unei abateri ξk este cu atât mai mică cu cât va-loarea abaterii este mai mare. Mai mult, valori egale ale abaterilor, dar opuse ca semn, sunt egal probabile. Rezultă de aici că funcţia de distribuţie a abaterilor depinde doar de modulul abaterii sau de pătratul ei :
f = f(ξ2)
Împărţind domeniul de valori pe care le ia abaterea în intervale Δξ egale între ele şi repre-zentând numărul valorilor experimentale ΔN din fiecare interval în funcţie de abaterea ξ co-respunzătoare, obţinem graficul alăturat. Se ob-servă că numărul cel mai mare de determinări furnizează valori ale abaterii cuprinse în jurul lui zero, în intervalul - ξmax/2 şi ξmax/2. Când numărul determinărilor este extrem de mare, N → ∞, probabilitatea ca abaterea să se găsească în intervalul de valori (ξ, ξ + dξ) se poate scrie ca o funcţie continuă : ξπ=ξξ=Δξ−∞→dead)(fNNlimaN2
Un asemenea tip de distribuire a abaterilor se numeşte distribuţia normală a lui Gauss sau „clopotul” lui Gauss. Constanta reală şi pozitivă a este o mărime care ca-racterizează precizia determinărilor (pentru valori mici ale lui a clopotul lui Gauss es-
te mai larg, ceea ce înseamnă că există multe valori ale lui ξ care se abat semnificativ de la valoarea nulă). Aria de sub clopot reprezintă probabilitatea unei valori a lui ξ cuprinsă între -∞ şi +∞, adică evenimentul cert. Prin urmare, mărimea ariei este unita-ră.
Preview document
Conținut arhivă zip
- Caiet de Lucrari Practice.pdf