Cursuri PSS

CURS NR.1

1.CONSTRUCŢII SUDATE DIN TABLĂ

1.1.Teoria matematicã a rezervoarelor

Formele obişnuite ale rezervoarelor metalice sunt în general suprafeţe obişnuite prin rotaţia unei curbe plane meridian în jurul unui ax mare care se aflã în planul curbei.

Grosimea peretelui fiind foarte mică în raport cu dimensiunile rezervorului, mantaua se considerã ca o membranã a cãrei formã este determinatã de suprafeţa medianã, obţinutã prin împãrţirea în douã a grosimilor peretelui. Din acelaşi motiv se poate neglija rezistenţa normalã pe suprafaţa medianã ca fiind micã faţã de celelalte rezistenţe şi se poate considera cã punctele care se aflã pe normala la suprafaţa medianã deformatã.

Se mai considerã de asemenea cã deformaţiile sunt mici în raport cu grosimea pereţilor ceea ce permite scrierea ecuaţiilor de echilibru pentru starea nedeformatã a pânzei adicã efectuarea calculelor în aproximaţia I. Din aceasta rezultã valabilitatea principiului simplificator al suprapunerii efectelor.

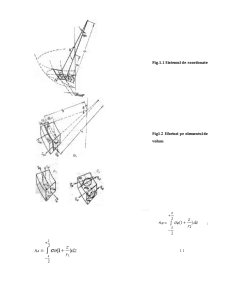
Punctele suprafeţei mediane sunt determinate printr-un plan median care face unghi θ cu planul meridian de referinţã şi prin unghiul φ format de normala la suprafaţa medianã cu axa de rotaţie ( Fig. 1.1)

Pentru un punct oarecare al suprafeţei vom însemna:

r1 – raza de curburã a curbei suprafeţei

r2 – lungimea normalei mãsuratã de la punctul considerat pânã la axa de rotaţie

r0 – raza cercului paralel

Considerând un element infinitezimal, determinat de meridianele infinit vecine θ şi θ +dθ şi de paralele cu unghiul normalelor corespunzãtoare φ şi φ+dφ pe suprafeţele elementului apar tensiunile σ şi τ ( arãtate în Fig.1.2.)

Aceste tensiuni normale şi tangenţiale, aşa cum se obişnuieşte şi în teoria plãcilor plane, pot fi înlocuite prin forţe şi momente raportate la unitatea de lungime. Aceste mãrimi statice unitare sunt arãtate în figura 1.2b şi 1.2c iar expresiile lor sunt:

Fig.1.1 Sistemul de coordonate

Fig1.2 Eforturi pe elementul de volum

Forţele nφ şi nθ sunt considerate pozitive ca forţe de tracţiune, iar sensul pozitiv al momentelor şi forţelor tãietoare este arãtat în figura 1.2c. Ordonata „z” se considerã pozitivã când se mãsoarã în afara suprafeţei mediane.

1.1.1 Stadiul de membranã

O primã simplificare a relaţiilor de mai sus se poate obţine prin considerarea suprafeţelor elementului infinitezimal ca dreptunghiuri şi prin neglijarea termenilor şi ca fiind foarte mici.

Aceasta înseamnã cã eforturile unitare normale σ şi cele tangenţiale τ variazã liniar pe grosimea peretelui.

În anumite cazuri se poate considera mai departe cã eforturile unitare sunt uniform repartizate pe grosimea peretelui s adicã independent de z.