Extras din laborator
Obiectivele lucrării :
Însușirea metodelor tehnologice de sinteză chimică din soluții SCS și cercetarea practica a nanostructurilor de ZnO.
Derularea lucrarii:
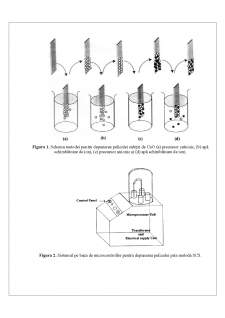
Peliculele columnare de oxizi semiconductori sunt depuse pe diferite tipuri de substraturi (în special pe sticlă comercială pentru microscoape 76 mm × 25 mm × 1 mm, ceramică, plachete de SiO2 /Si, cuarț etc.) utilizând metoda sintezei chimice din soluții (SCS). Un ciclu de depunere SCS constă din trei-patru etape: (1) scufundarea substratului, în prealabil curățit și sensibilizat cu ajutorul soluției de SnCl2 - 2H2 O/HCl [26], în soluția complexă cu anioni (A- ) menținută la temperatura necesară; (2) clătirea într-un vas cu apă deionizată (această etapă poate fi exclusă, în funcție de morfologia finală solicitată a nanocoloanelor); (3) scufundarea substratului în soluția complexă cu cationi (K+) pentru reacția cu anionii deja adsorbiți pe substrat în pasul (1); (4) clătirea într-un vas cu apă deionizată pentru înlăturarea produselor ce nu au intrat în reacție, cu scopul de a obține pelicule de o calitate cât mai înaltă (etapa dată poate fi doar finală, în funcție de morfologia finală solicitată a nanocoloanelor crescute SCS). Procesul unui ciclu de depunere SCS este ilustrat în fi gura 1. Astfel, prin reglarea numărului ciclurilor SCS se poate obține grosimea necesară a peliculei columnare depuse, precum și a cristalitelor ce o formează. Pentru a automatiza procesul de depunere SCS și a mări repetabilitatea proprietăților peliculelor, a fost elaborat un sistem încorporat automatizat în baza unui microprocesor (MCU) (figura 2). Sistemul respectiv permite de a instala cu precizie numărul de cicluri SCS, viteza de deplasare a substratului dintr-un vas în altul, timpul de menținere în fi ecare vas, rotirea sau nu a cleștelui din teflon care menține substratul și temperatura în vasele cu soluții. Menținerea în etapa (2) poate fi instalată de la 0 la x s, astfel numărul etapelor se reduce de la 4 la 3. Ca rezultat, sistemul încorporat permite excluderea erorilor umane și, respectiv, repetabilitatea mai înaltă a proprietăților peliculelor depuse prin metoda SCS.[1]
Preview document
Conținut arhivă zip
- Cresterea SCS a nanostructurilor ZnO columnare.docx