Modelul linear de regresie simplă

Se cunosc următoarele date privind capacitatea de cazare turistică în funcţiune (mii locuri-zile) şi numărul de înnoptări în structurile de primire turistică (mii) în perioada 1989-2002:

Tab. 1

Anul

Capacitate de cazare turistica în funcţiune

(mii locuri-zile)

Numărul de înnoptări în structurile de primire turistică cu funcţiuni de cazare turistică

(mii)

0 1 2

1989 78358 52217

1990 75922 43392

1991 63024 30767

1992 54770 24916

1993 56334 23609

1994 52155 22136

1995 52440 22951

1996 52539 20678

1997 50927 18451

1998 52064 18023

1999 50175 16510

2000 49097 16487

2001 50082 16962

2002 49652 16117

Se cere:

1.

a) să se specifice modelul econometric ce descrie legătura dintre cele două variabile;

b) să se estimeze parametrii modelului şi să se calculeze valorile teoretice ale variabilei endogene;

c) să se verifice ipotezele de fundamentare a metodei celor mai mici pătrate;

d) să se verifice semnificaţiile estimatorilor şi verosimilitatea modelului;

e) presupunînd că în anul 2003 numărul de înnoptări va atinge valoarea de 17100-10N să se estimeze capacitatea de cazare turistică în funcţiune în acest caz.

2. Soluţionarea problemei cu ajutorul pachetului EViews.

Rezolvare:

a) Bazîndu-ne pe datele problemei putem construi modelul econometric de forma:

y = f(x) + u

Unde:

y = valorile reale ale variabilelor dependente;

x = valorile reale ale variabilelor independente;

u = variabila reziduală, ce reprezintă influenţele celorlalţi factori (întîmplători) ai variabilei y, nespecificaţi în model, cu influenţe nesemnificative asupra variabilei y;

Analizînd datele problemei putem specifica că:

y - capacitatea de cazare turistică în funcţiune, reprezentînd variabila rezultativă (endogenă);

x - numărul de înnoptări, reprezentînd variabila exogenă, respective factorul considerat prin ipoteza de lucru cu influenţa cea mai puternică asupra variabilei y.

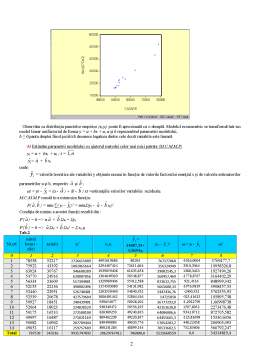
Construim coreolograma (fig.1):

Observăm ca distribuţia punctelor empirice (xt,yt) poate fi aproximată cu o dreaptă. Modelul econometric se transformă într-un model linear unifactorial de forma y = a + bx + u, a şi b reprezentînd parametrii modelului,

b ≥ 0,panta dreptei fiind pozitivă deoarece legatura dintre cele două variabile este lineară.

b) Estimăm parametrii modelului cu ajutorul metodei celor mai mici patrate (M.C.M.M.P)

yt = a + bxt + ut ; t =

= + xt

unde:

= valorile teoretice ale variabilei y obţinute numai în funcţie de valorile factorului esenţial x şi de valorile estimatorilor parametrilor a şi b, respectiv şi ;

ut = yt – = (a - ) + (b - ) xt =estimaţiile valorilor variabilei reziduale.

M.C.M.M.P constă în a minimiza funcţia:

F( , ) = min ∑( yt – )2 = minΣ(yt – - xt)2

Condiţia de minim a acestei funcţii rezultă din :

F′( ) = 0 => n + Σxt = Σyt

F′( ) = 0 => Σxt + Σxt2 = Σ xt yt

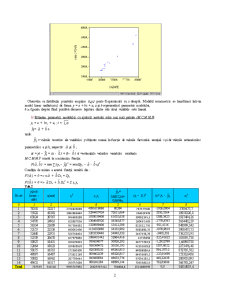
Tab.2

Nr.crt yt(mii locuri - zile) xt(mii) xt2 xt yt =

34887,24+ 0,8694xt (xt – )2

ut= yt -

ut2

0 1 2 3 4 5 6 7 8

1 78358 52217 2726615089 4091619686 80284 767377060 -1926,0004 3709477,7

2 75922 43392 1882865664 3294407424 72611,664 356324949 3310,3364 10958326,8

3 63024 30767 946608289 1939059408 61635,658 39082145,3 1388,3423 1927494,26

4 54770 24916 620807056 1364649320 56548,877 160457,469 -1778,8767 3164402,29

5 56334 23609 557384881 1329989406 55412,588 821612,755 921,4116 848999,342

6 52155 22136 490002496 1154503080 54131,982 5661680,33 -1976,9819 3908457,53

7 52440 22951 526748401 1203550440 54840,532 2447436,76 -2400,532 5762553,93

8 52539 20678 427579684 1086401442 52864,416 14725858 -325,41625 105895,738

9 50927 18451 340439401 939654077 50928,292 36777293,9 -1,2922799 1,66998738

10 52064 18023 324828529 938349472 50556,195 42151628,8 1507,8052 2273476,48

11 50175 16510 272580100 828389250 49240,813 64086886,6 934,18712 872705,582

12 49097 16487 271821169 809462239 49220,817 64455665,3 -123,81698 15330,6456

13 50082 16962 287709444 849490884 49633,776 57054283,2 448,22438 200905,093

14 49652 16117 259757689 800241284 48899,144 70533602,5 752,85606 566792,247

Total 787539 343216 9935747892 20629767412 786808,8 1521660559 0,0 34314819,4

Tab.2 (continuare)

yt –

(yt – ) 2

( – ) 2

xt –

(xt – )

ut-1 (ut- ut-1) 2 utut-1 (xt – ) (yt – )

9 10 11 12 13 14 15 16 17

22105,21 488640498,6 577499054,1 27701,57 -53353235 - - - 612349053,8

19669,21 386877990,6 267612758,5 18876,57 62487797 -1926,0004 27419223 -10085186,77 371287247,5

6771,21 45849342,9 28975267,91 6251,57 8679319,1 3310,3364 3694061 -6362447,03 42330702,97

-1482,79 2198653,474 87667,51157 400,57 -712564,64 1388,3423 10031276 -4397184,111 -593963,3086

81,21 6595,760204 705939,4008 -906,43 -835195,12 -1778,8767 7291557 -4803479,94 -73611,06429

-4097,79 16791847,76 4497826,573 -2379,43 4704090 921,4116 8400685 -2670613,392 9750398,606

-3812,79 14537334,9 1994472,659 -1564,43 3755464,3 -1976,9819 179394,7 837350,8814 5964837,613

-3713,79 13792204,33 11481078,36 -3837,43 1248762,1 -2400,532 4306105 -4981381,762 14251403,85

-5325,79 28363993,47 28350278,95 -6064,43 7836,941 -325,41625 105056,3 -105475,2069 32297873,04

-4188,79 17545925,76 32451194,59 -6492,43 -9789319,7 -1,2922799 2277375 -1950,17634 27195419,88

-6077,79 36939479,19 49167821,45 -8005,43 -7478569,6 1507,8052 329037,7 -864904,3238 48655313,72

-7155,79 51205269,19 49448644,27 -8028,43 994055,96 934,18712 1119373 -988373,8031 57449748,89

-6170,79 38078596,33 43811346,33 -7553,43 -3385631,5 -123,81698 327231,3 -70828,43363 46610621,49

-6600,79 43570372,05 54076109,49 -8398,43 -6322808,9 448,22438 92800,46 136543,3459 55436263,33

0,0 1184398104 1150159460 0,0 0,0 752,85606 65573176 -34360609,58 1322911310

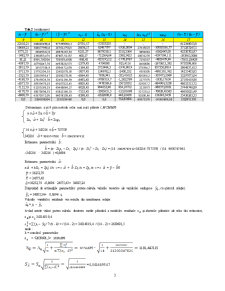
Determinam a şi b prin metoda celor mai mici pătrate ( MCMMP)

n ּ + Σxt ּ = Σy

Σxt • + Σxt2 • = Σxtyt

14 ּ + 343216 ּ = 787539

343216 • + 9935747892 • = 20629767412

Estimarea parametrului :

= (n • Σxtyt – Σxt • Σyt) / (n • Σxt2 – Σxt • Σxt) = (14 •20629767412–343216•787539) / (14 •9935747892

–343216 • 343216 ) =0,8694

Estimarea parametrului :

n + bΣxt = Σyt| 1/n <=> + Σxt /n = Σyt /n <=> = –

= 56252,79

= 24575,43

=56252,79 –0,8694• 24575,43= 34887,24

Dispunînd de estimaţiile parametrilor putem calcula valorile teoretice ale variabilei endogene , cu ajutorul relaţiei:

= 34887,24+ •0,8694 xt

Valorile variabilei reziduale vor rezulta din următoarea relaţie:

= yt –

Avînd aceste valori putem calcula abaterea medie pătratică a variabilei reziduale s şi abaterile pătratice ale celor doi estimatori, s şi s :34314819,4