Cuprins
- Cap. 1. INTRODUCERE 3
- Cap. 2. OSCILATORUL ARMONIC 3
- Cap 3. REPREZENTAREA COMPLEXĂ A OSCILAŢIILOR SINUSOIDALE 9
- Cap. 4. COMPUNEREA OSCILAŢIILOR ARMONICE PARALELE 13
- Cap. 5 COMPUNEREA OSCILAŢIILOR ARMONICE PERPENDICULARE 18
- Cap. 6. OSCILAŢIILE AMORTIZATE 20
- Cap. 7. OSCILAŢIILE FORŢATE 25
- Cap. 8. REZONANŢA 31
- Cap. 9. OSCILAŢIILE SISTEMELOR CU MAI MULTE GRADE DE LIBERTATE 38
- Cap. 10. ANALIZA ARMONICĂ (FOURIER) 42
Extras din licență
Cap. 1. INTRODUCERE
Oscilaţiile prezintă o importanţă covârşitoare pentru fizică şi tehnică, iar dintre ele cele simple, sinusoidale au rol fundamental, fiindcă orice oscilaţie poate fi obţinută prin suprapunerea unor oscilaţii sinusoidale (teorema Fourier).
Cap. 2. OSCILATORUL ARMONIC
Oscilatorul armonic este un punct material care execută oscilaţii sinusoidale pe o dreaptă sub acţiunea unei forţe atractive proporţionale cu distanţa până la centrul atractiv (centrul mişcării).
a) Reamintim relaţiile stabilite mai înainte:
Elongaţia :
unde: A este amplitudinea mişcării, - faza mişcării, - faza iniţială, - frecvenţa unghiulară - frecvenţa, T – perioada mişcării.
Viteza:
viteza este defazată înainte cu /2 (sau T/4) faţă de elongaţie.
Acceleraţia :
acceleraţia este defazată cu (sau T/2) faţă de elongaţie, adică este în opoziţie de fază cu elongaţia (fig. 1).
Forţa :
Ecuaţia diferenţială a oscilatorului armonic:
. (6)
Mişcarea armonică poate fi reprezentată geometric prin proiecţia pe o axă a unui vector de modul A care se roteşte în sens trigonometric cu viteza unghiulară ω (fig. 2). Proiecţia A' a extremităţii acestui vector execută mişcarea armonică ( fig. 1).
Fig. 1
Analog, viteza şi acceleraţia în mişcarea armonică sunt date în fiecare moment de proiecţiile extremităţii vectorilor de modul ωA, ω2A, defazaţi cu π/2, respectiv π faţă de vectorul A (fig. 2). Ne putem imagina de asemenea că în loc să se rotească vectorii, se roteşte axa OX în sens invers.
Fig. 2
b) Energia cinetică, Ec, potenţială U şi totală E a oscilatorului armonic sunt :
Energia totală este constantă (se conservă) şi este proporţională cu pătratul amplitudinii şi cu pătratul frecvenţei.
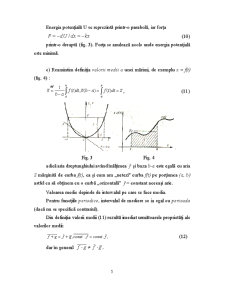
Energia potenţială U se reprezintă printr-o parabolă, iar forţa
(10)
printr-o dreaptă (fig. 3). Forţa se anulează acolo unde energia potenţială este minimă.
c) Reamintim definiţia valorii medii a unei mărimi, de exemplu x = f(t) (fig. 4) :
Fig. 3 Fig. 4
adică aria dreptunghiului având înălţimea şi baza b-a este egală cu aria S mărginită de curba f(t), ca şi cum am „netezi" curba f(t) pe porţiunea (a, b) astfel ca să obţinem cu o curbă „orizontală" = constant aceeaşi arie.
Preview document
Conținut arhivă zip
- Compunerea Oscilatiilor Armonice Perpendiculare
- 3940._Cuprins.doc
- Compunerea Oscilatiilor Armonice Perpendiculare.doc