Mecanisme

Pentru mecanismul din figură se cere:

1. Analiza configurației și a cinematicii

1.1. Clasificarea mecanismului, rezolvarea configurației prin metoda grafică și analitică pentru o rotație completă a manivelei.

1.2. Rezolvarea cinematicii mecanismului prin metoda analitică pentru o rotație completă a manivelei.

2. Analiza dinamică

2.1. Calculul momentului de inerție redus a mon=mentului rezistent redus și determinarea variației energiei cinetice

2.2. Alegerea motorului electric și al reductorului.

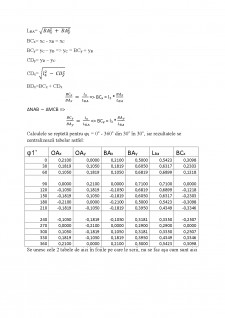
2.3. Calculul momentului de inerție a volantului pe baza diagramei ΔE(J1*)

2.4. Analiza mișcării în faza de pornire.

Se dau: l1=0,21 m; l3=0,8 m; l4=0,3 m; m1=1,5 kg; m2=2,1 kg; m3=6,4 kg; m4=3,1 kg; m5=15 kg; n1= 60: a=0,5 m; b=0,9 m; F5u=13000 N; δ=1/11;

1. Analiza configurației și a cinematicii

1.1. Gradul de mobilitate și clasificarea mecanismului

7 cuple cinematice; M=3n-2C5-C4

M=3*5-2*7=1

Mecanismul este: plan, cu bare de acționare, familia mecanismlui este 3.

Clasa și ordinul mecanismului.

Rezolvarea configurației prin metoda grafică.

Pentru reprezentarea grafică a mecanismului în 12 poziții de funcționare se procedează astfel:

- se alege scara de reprezentare pentru lungimi și se calculează lungimile pe desen ale elementelor: S= l_r/l_d = 0,005 m/mm

ld = l_r/S ; l1d=0,21/0,005= 42 mm; l3d=0,8/0,005=160 mm; l4d=0,3/0,005=60 mm; ad=0,5/0,005=100 mm; bd=0,9/0,005=180 mm;

- se reprezintă sistemul de axe xOy

- se reprezintă articulațiile fixe din O și B

- cu vârful în O și cu raza l1d se desenează cercul ce reprezintă traiectoria punctului A

- se împarte cercul în 12 poziții succesive (A1, A2, ... , A12) din 30˚ în 30˚

- se trasează semidreptele BAi și se prelungește până la intersecția cu arcul de cerc având centrul în B și raza l3d rezultând puntul Ci

- se reprezintă traiectoria punctului D (paralelă cu axa x și la distanța de bd-ad)

- din punctele Ci se construiect arce de cerc de rază l4d care intersectează traiectoria lui D în punctele Di