Cuprins
- 1. ARGUMENT
- 2. GRAFURI
- 3. DRUMURI INTR-UN GRAF
- a. Drumuri minime
- b. Drumuri maxime
Extras din proiect
Am ales aceasta tema in scopul de a va arata ca si in informatica exista distante (adica ”drumuri”) atat minime cat si maxime intre elementele unui graf fie el orientat sau neorientat.
GRAFURI
Fie o mulţime finită x={x1,x2,…,xn}.Fie Γ XxX, unde XxX este produsul cartezian al mulţimii X cu ea însăşi.
Definiţie. Se numeşte graf orientat perechea ordonată G=(x, Γ).
- Elementele xi є x se numesc noduri sau vârfuri.
- Elementele mulţimii Γ se numesc arce.Un arc (xk,xi)єΓ se notează şi cu [xk,xi].Prin abuz de notaţie, vom scrie: [xk,xi]єΓ.
În concluzie, graful este: G=(x, Γ)= ({x1,x2,x3,x4},{[x1,x2],[x2,x1],[x3,x4],[x3,x2],[x3,x3]}).
Un graf orientat poate fi reprezentat printr-un desen, aşa cum rezultă din imaginea alăturată.
Dacă în graful G=(x, Γ) [x,y]єΓ vom spune că x şi y sunt adiacente, iar vârfurile x şi y sunt incidente cu muchia [x,y].
Dacă Γ=Ø (mulţimea vidă),graful G=(x, Γ) se numeşte graf nul şi reprezentarea lui în plan se reduce la puncte izolate.
Definiţie.Un graf parţial al unui graf orientat dat G=(x, Γ) este un graf G1=(x, Γ1) unde Γ1 Γ un graf partial se obtine dintr-un graf suprimand anumite arcuri.
G=(x, Γ) G1=(x, Γ1)
Definiţie: Un subgraf al unui graf orientat G=(x, Γ) este un graf H=(x, Γ1), unde ,iar muchiile din sunt toate muchiile din care au ambele extremităţi în mulţimea Y.
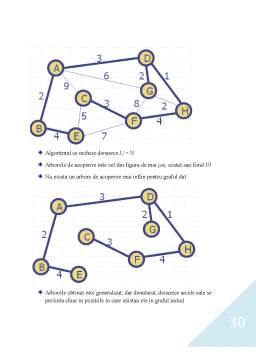
DRUMURI INTR-UN GRAF
Fie G=(X,U) un graf orientat.Se numeste drum in graful G ,D=(x1,x2,x3,...,xk) o succesiune de varfuri cu proprietatea ca [xi,xi+1]€U , unde 1<=i<=k-1.
Observatii:
- Varfurile x1 si xk sunt numite extremitatile drumului.
Preview document
Conținut arhivă zip
- Drumuri de Cost Minim si Maxim.doc
Alții au mai descărcat și
Rezultatele din testul 3DS Max 7 SPECapc Test Testul alaturat consta in crearea modelelor 3D, modificarea si randarea scripturilor. Conform...
Introducere O semnatura digitala reprezinta o informatie care il identifica pe expeditorul unui document. Semnatura digitala este creata prin...
Caracteristici generale ale placii de baza Placa de baza este un dizpozitiv ‘de baza’ un ‘pamânt’ pe care ‘se planteaza’ celelalte componente ....
Acest sistem calculeaza gradul de avariere a unei cladiri în cazul unui cutremur, precum si posibila necesitate a reconstructiei cladirii (partiala...
Te-ar putea interesa și
“Diferența dintre școală și viață? În școală, înveți o lecție, apoi dai un test. În viață, ai de dat un test care te învață o lecție.” (Tom...
1. Introducere 1.1 Ce este un algoritm?Tipuri de algoritmi folositi pentru calcularea drumului optim Scurt istoric: “Originile teoriei...
Prezentarea agentiei (vezi anexa 1) Agentia de turism este unitatea comerciala specializata care organizeaza, ofera si vinde servicii turistice...
Pusi in fata unei probleme pentru care trebuie sa elaboram un algoritm, de multe ori "nu stim cum sa incepem". Ca si in orice alta activitate,...
I.METODA DIVIDE ET IMPERA 1.Notiuni introductive Asa cum spune si denumirea metodei (imparte si stapaneste), metoda se bazeaza pe impartirea unei...
Prezentarea algoritmului standard Algoritmul Dijkstra este un algoritm care calculeaza drumurile minime de la un nod al unui graf la toate...
1. Preliminarii 1.1. Algoritmi Toti algoritmii descrisi în cadrul acestei lucrari folosesc structuri de date de tip graf. Unele descrieri sînt...
