Regresie și Serii de Timp

Prezentarea problemei:

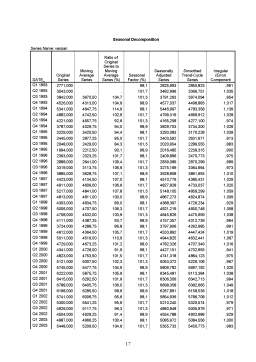
Se înregistrează un eşantion de n=68 de cazuri, cu privire la volumul vânzarilor unei firme influenţate de preţul produselor şi promoţia făcută acelui produs. Dorim să exprimăm legătura dintre volumul vânzarilor şi preţul produselor şi promoţiile printr-o regresie liniară multiplă. Regresia liniară multiplă este un caz al analizei de regresie, deoarece într-un astfel de model variabila dependentă ar fi explicată de două variabile independente, în cazul nostru.

Se înţelege că, în exemplul dat, volumul vânzarilor nu depinde numai de preţul produselor şi de promoţie, ci şi de un ansamblu de alte variabile pe care le exprimăm sintetic printr-o variabilă numită eroare sau reziduu.

Forma modelului de regresie liniară multiplă este:

Variabilele modelului sunt:

Y=volumul vânzarilor care reprezintă variabila dependentă (rezultativă),

=preţul produselor care reprezintă variabila independentă (factorială),

=promoţia pentru acel produs care reprezintă cealaltă variabilă factor.

= variabila aleatoare, variabila care însumeaza influenţa altor variabile asupra preţului, dar care nu sunt specificate expres în model. Variabila exprimă abaterile între valorile observate şi valorile estimate prin model.

Parametrii modelului de regresie simplă liniară, numiţi şi coeficienţi de regresie, sunt:

- ordonata la origine - arată valoarea medie a variabilei Y când şi sunt egale cu zero

- panta dreptei - arată variaţia medie a variabilei dependente, Y, la o

variaţie absolută cu o unitate a variabilei , adică variaţia variabilei Y este proporţională cu variaţia variabilei când este ţinut constant

panta dreptei - arată variaţia medie a variabilei dependente, Y, la o

variaţie absolută cu o unitate a variabilei , adică variaţia variabilei Y este proporţională cu variaţia variabilei când este ţinut constant.

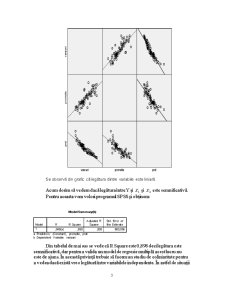
Acum dorim să aproximăm modleul legăturii dintre variabile folosind metoda grafică.

Se observă din grafic că legătura dintre variabile este liniară.

Acum dorim să vedem dacă legătura între Y şi şi este semnificativă.

Pentru aceasta vom volosi programul SPSS şi obţinem:

Model Summary(b)

Model R R Square Adjusted R Square Std. Error of the Estimate

1 ,948(a) ,898 ,895 680,056

a Predictors: (Constant), promotie, pret

b Dependent Variable: vanzari

Din tabelul de mai sus se vede că R Square este 0,898 deci legătura este semnificativă, dar pentru a valida un model de regresie multiplă acest lucru nu

este de ajuns. În această privinţă trebuie să facem un studiu de coliniaritate pentru a vedea dacă există vreo legătură între variabilele independente. În astfel de situaţii se calculează statisticile toleranţei considerând numai variabilele independente, variabila dependentă fiind exclusă din model. Toleranţa fiecărei variabile se calculează după relaţia;

Toleranţa=1- unde este pătratul coeficientului de corelaţie multiplă a variabilei cu toat celelalte variabile independente.

Toleranţa poate lua valori de la 0 la 1. Cu cât valoarea toleranţei este mai aproape de zero cu atât variabila independentă este mai explicată printr-o combinaţie liniară a celelante variabile independente.