Extras din proiect
INTRODUCERE
În analiza matematică, integrala unei funcții este o generalizare a noțiunilor de arie, masă, volum și sumă. Procesul de determinare a unei integrale se numește integrare. Spre deosebire de noțiunea înrudită de derivată, există mai multe definiții posibile ale integralei, fiecare cu suportul său tehnic.
Acestea sunt însă compatibile. Oricare două moduri de integrare a unei funcții vor da aceleași rezultate când ambele sunt definite. Termenul "integrală" se poate referi și la noțiunea de primitivă a unei funcții, adică o funcție F a cărei derivată este funcția dată f. În acest caz, se numește integrală nedefinită, pe când integralele discutate în acest articol sunt numite integrale definite.
Principiile integrării au fost enunțate de Isaac Newton și Gottfried Wilhelm Leibniz la sfârșitul secolului al XVII-lea.
Prin teorema fundamentală a calculului integral, pe care au dezvoltat-o independent unul de altul, integrarea este legată de derivare, iar integrala definită a unei funcții poate fi ușor calculată odată ce este cunoscută o primitivă a ei. Integralele și derivatele au devenit uneltele de bază ale analizei matematice, cu numeroase aplicații în știință și inginerie.
O definiție riguroasă a integralei a fost dată de Bernhard Riemann. Ea este bazata pe o trecere la limită prin care se aproximează aria unei regiuni curbilinii prin descompunerea acesteia în zone verticale subțiri.
Din secolul al XIX-lea, au înceut să apară tipuri de integrale mai sofisticate, în care atât tipul funcției cât și domeniul peste care se face integrarea au început să fie generalizate. O integrală curbilinie este definită pentru funcții de două sau trei variabile, iar intervalul de integrare [a,b] este înlocuit de o anumită curbă care leagă două puncte din plan sau din spațiu. Într-o integrală de suprafață, curba este înlocuită de o bucată de suprafață din spațiul tridimensional. [6.]
Capitolul 1. Aplicații ale integralei definite, Aplicații geometrice
§1.1. Calcularea ariilor figurilor plane în coordonate carteziene rectangulare Dacă funcția f(x) este nenegativă și continuă pe [a,b], atunci, reieșind din sensul geometric al integralei nedefinite, aria trapezului curbiliniu, mărginit de curba y=f(x), axa Ox și dreptele x=a, x=b, este egală cu S =∫_a^b▒f(x)dx
Dacă funcția f(x) este nepozitivă și continuă pe [a,b], atunci
∫_a^b▒〖f(x)dx≤0〗
Aria trapezului curbiliniu este egală cu modulul acestei integrale.
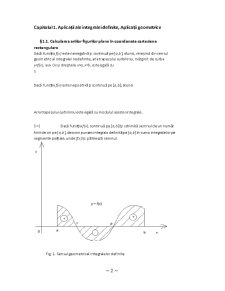
S =|∫_a^b▒〖f(x)dx|〗 Dacă funcția f(x), continuă pe [a,b] își schimbă semnul de un număr finit de ori pe [a,b], descompunem integrala definită pe [a,b] în suma integralelor pe segmente parțiale, unde f(x) își păstrează semnul.
Fig. 1. Sensul geometric al integralelor definite
[a,c], [c,p], [p,b]. (fig.1)
Atunci S=s_1 〖+s〗_2 〖+s〗_3,unde〖 S〗_1=∫_a^c▒〖f(x)dx ,〗 〖 S〗_2= -∫_c^p▒〖f(x)dx ,〗 〖 S〗_3=∫_p^b▒〖f(x)dx ,〗 =>
S = ∫_a^c▒〖f(x)dx -∫_c^p▒〖f(x)dx+ ∫_p^b▒〖f(x)dx 〗 〗〗= ∫_c^b▒〖|f(x)dx|.〗
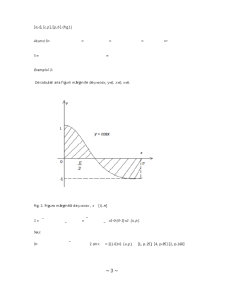
Exemplul 1:
De calculat aria figurii mărginite de y=cosx, y=0, x=0, x=π.
Bibliografie
1. Șcerbațchi, Ion C. Analiză matematică (probleme). Volumul II. Chișinău: Editura Tehnica, 1998. 362 P.
2. Miron, S. Curs de analiză matematică, Chișinău, 1992. 210 P.
3. Piscunov, N. S. Calcul diferențial și integral. Volumul I. Chișinău: Lumina, 1991. 432 P.
4. Berman, G. N. Culegeri de probleme de analiză matematică. Chișinău: Lumina, 1968. 476 P.
5. Roșculeț, M. Analiză matematică, Bucurști: Dacia, 1979. 320 P.
6. http://ro.wikipedia.org/wiki/Integral%C4%83
Preview document
Conținut arhivă zip
- Integrale definite.docx