Modele de predicție a funcționării unui sistem mecanic pe baza aplicării lanțurilor Markov

Rezumat

Lucrarea intitulată „Modele de predicţie a funcţionării unui sistem mecanic pe baza aplicării lanţurilor Markov” este structurată pe patru capitole şi prezintă, pe langă partea teoretică a proceselor stochastice de tip lanţ Markov şi aplicaţii practice ale acestora.

Capitolul 1 numit Procese stochastice şi lanţuri Markov cuprinde noţiuni teoretice privind Lanturile Markov, care, au fost denumite după matematicianul rus Andrei Markov. Într-un proces Markov, la fiecare moment sistemul îşi poate schimba sau păstra starea, în conformitate cu o anumită distribuţie de probabilitate. Schimbările de stare sunt numite tranziţii. Un exemplu simplu de proces Markov este parcurgerea aleatoare a nodurilor unui graf, tranziţiile fiind trecerea de la un nod la unul din succesorii săi, cu probabilitate egală, indiferent de nodurile parcurse până în acel moment. Practica oferă numeroase exemple, în care anumite valori caracteristice ale unui sistem, formând aşa numitele stări discrete ale sistemului, variază o dată cu timpul, astfel încât ele nu pot fi prevăzute cu exactitate. Un asemenea proces, în care una sau mai multe valori caracteristice lui variază aleator în timp, îl numim “proces stochastic”. Procesele stochastice permit modelarea matematică a numeroaselor component ale sistemelor tehnice, informatice, economice, sociale etc.

În acest capitol urmează sa fie redate succint principalele definiţii şi proprietăţi ale proceselor stochastice şi ale lanţurilor Markov (LM), clasificarea acestora în conformitate cu modul cum ele sunt "vizitate" în cursul timpului funcţionării lanţului. De asemenea, este prezentată şi noţiunea de agregare Markoviană, ce constă în a partiţiona spaţiul de stări Ω ale unui lanţ în subansambluri (Ωk)k=1,.,K în aşa mod încât, comportamentele de stări ale unor şi aceleaşi Ωk , să fie stochastic echivalente. În practică se întâlnesc deseori şi sisteme dinamice cu stări discrete, pentru care durata de aflare într-o oarecare stare i, fiind o variabilă aleatoare, depinde de această stare şi de starea următoare de trecere şi ea nu este necesar distribuită conform legii exponenţial-negative. Evoluţia sistemului este astfel definită de starea curentă şi de starea ce urmează. Acest tip de procese stochastice sunt numite procese semi-Markov.

Deoarece lanţurile Markov sunt procese stochastice, nu se poate şti cu exactitate ce se întâmplă în fiecare stare; de aceea, sistemul trebuie descris în termeni de probabilitate.

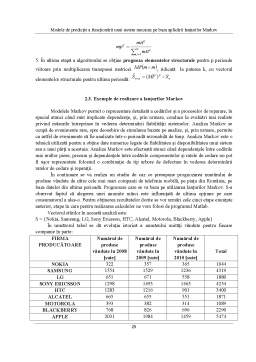
Capitolul 2 numit Analiza structurala a lanturilor Markov prezintă modele probabilistice de studiu a fiabilităţii bazate pe lanţuri Markov pe baza caroră funcţionarea oricărui element al unui sistem mecanic se caracterizează printr-o succesiune de stări care descriu regimurile de funcţionare normale sau de avarie. Datorită naturii probabilistice a stărilor prin care trece instalaţia respectivă, se poate admite că evoluţia procesului este descrisă de un proces aleatoriu. Evoluţia procesului respectiv este definită de o familie de variabile care descriu traiectoria procesului. Cunoaşterea stărilor sistemului la momentele consecutive t1, t2,.,tn, anterioare lui t, contribuie la cunoaşterea stării în momentul t prin colectarea unor informaţii referitoare la starea din momentele anterioare, dar cuprinse toate în starea cea mai recentă, respectiv starea din momentul tn. Trebuie ţinut cont de faptul că, în general, un sistem poate ajunge într-o anume stare prin mai multe succesiuni de stări, modul în care sistemul respectiv a ajuns aici influenţând funcţionarea sa ulterioară, şi deci şi indicatorii care caracterizează fiabilitatea sistemului pentru momentul tn. Procesul care are o asemenea evoluţie, caracterizată de faptul că, starea în care va trece sistemul depinde atât de starea în care se găseşte acesta cât şi de modul în care sistemul a ajuns în această stare, se numeşte proces Markov. De asemenea, în acest capitol se mai prezintă şi algoritmul de rezolvare a unui fenomen redat prin lanţul Markov, şi exemple de realizare a lanţurilor Markov cum ar fi: un studiu de caz ce presupune prognozarea numărului de produse vândute de către cele mai mari companii de telefonie mobilă pe piaţa din România, pe baza datelor din ultima perioadă, prognozare care se va baza pe utilizarea lanţurilor Markov.

Capitolul 3 este numit Procese Markov. Aici se prezintă faptul că procesele Markov sunt caracterizate prin aceea că, apariţia unei anumite stări este condiţionată doar de un număr determinat de stări anterioare. Dacă numărul acestor stări anterioare este r, atunci este vorba de un proces Markov de ordinul r.

Procesele Markov de ordinul 1 ocupă un loc important în studiul proceselor de trafic ce caracterizează reţeaua de telecomunicaţii în ansamblul ei. Procesele de naştere şi moarte ca subclasă importantă a proceselor Markov de ordinul 1 se adaptează perfect modului de apariţie şi deservire a traficului în sistemul global de telecomunicaţii. Aceste procese sunt caracterizate de un spaţiu discret de stări şi de un parametru temporal continuu.

Pe langă partea teoretică a proceselor Markov, în acest capitol sunt prezentate şi patru aplicaţii ale acestor procese.

Capitolul 4 numit Programul Toolkit şi Analiza de tip Markov, prezinta programul Toolkit şi modul de utilizare a acestuia, crearea unui proiect Markov, ce foloseste modulul ITEM Toolkit Markov pentru a modela şi analiza un sistem simplu de două componente de aşteptare. Sistemul constă din două componente identice care operează în modul de „aşteptare la cald”. Se presupune că cedările asociate componentei de aşteptare nu sunt detectate până când nu este se pune o întrebare în acest sens. Deasemea, în acest capitol, se prezintă şi alte aplicaţii necesare înţelegii modului de aplicare şi utilizare a lanţurilor Markov în predicţia funcţionării sistemelor dinamice.

Capitolul 1. Procese stohastice şi lanţuri Markov

În matematică, un proces Markov, sau un lanţ Markov, este un proces stohastic care are proprietatea că, dată fiind starea sa prezentă, stările viitoare sunt independente de cele trecute. Această proprietate se numeşte proprietatea Markov. Cu alte cuvinte, starea curentă a unui astfel de proces reţine toată informaţia despre întreaga evoluţie a procesului. Lanţurile Markov au fost denumite după matematicianul rus Andrei Markov. Într-un proces Markov, la fiecare moment, sistemul îşi poate schimba sau păstra starea, în conformitate cu o anumită distribuţie de probabilitate. Schimbările de stare sunt numite tranziţii. Un exemplu simplu de proces Markov este parcurgerea aleatoare a nodurilor unui graf, tranziţiile fiind trecerea de la un nod la unul din succesorii săi, cu probabilitate egală, indiferent de nodurile parcurse până în acel moment. Practica oferă numeroase exemple în care, anumite valori caracteristice ale unui sistem, formând aşa numitele stări discrete ale sistemului, variază o dată cu timpul, astfel încât, ele nu pot fi prevăzute cu exactitate. Un asemenea proces în care una sau mai multe valori caracteristice lui variază aleator în timp îl numim “proces stohastic”.

Noţiuni şi definiţii generale

Procesele stohastice permit modelarea matematică a numeroaselor componente ale sistemelor tehnice, informatice, economice, sociale etc.

În cele ce urmează vom reda succint principalele definiţii şi proprietăţi ale proceselor stohastice şi ale lanţurilor Markov (LM).

Definiţia 1.1. Un proces stohastic X este o familie de variabile aleatoare(X_τ )_τϵτ definite pe acelaşi spaţiu de probabilitate cu valori reale, în acelaşi spaţiu de valori Ω şi indexate după un parametru τ∈τ⊆R.

Un proces stohastic se reprezintă prin:

{Xτ∈Ω,τ∈τ} (1.1)

De obicei, precizarea mulţimii τ coincide cu intervalul de timp al evoluţiei diverselor clase de procese stohastice. Astfel, dacă τ ={τ1,τ2,.,τn} este o mulţime finită, atunci procesul stohastic este echivalent cu un vector aleator, care determină vectorul de stare al sistemului studiat.

În termeni probabilistici, a descrie evoluţia unui proces stohastic înseamnă cunoaşterea probabilităţilor tuturor evenimentelor de forma: "la momentul τ procesul stohastic se găseşte în starea (Xτ=x)", precum şi a probabilităţilor de realizare simultană a unui număr de astfel de evenimente pentru diverse momente τi∈τ şi diverse mulţimi ei⊆R, 1≤i≤n. Cu alte cuvinte, este necesar să fie cunoscute probabilităţile de forma:

Pr(Xτ1∈e1,.,Xτn∈en) (1.2)

pentru orice n∈N, orice τi∈τ şi orice ei⊆R, 1≤i≤n. Acest fapt se manifestă prin cunoaşterea funcţiilor de repartiţie n – dimensionale: