Cuprins
- INTRODUCERE 6
- CAPITOLUL 1 8
- ELEMENTE DE PROBABILITĂŢI ŞI STATISTICĂ MATEMATICĂ 8
- 1.1. Elemente de teoria probabilităţilor 8
- 1.1.1. Definirea termenului de probabilitate 8
- 1.1.2. Scheme clasice de probabilitate 10
- 1.1.3. Legi de repartiţie 11
- 1.1.4. Variabile aleatoare 16
- 1.2. Elemente de statistică matematică 20
- 1.2.1. Categorii de indicatori şi interpretarea acestora 20
- 1.2.2. Corelaţie şi regresie 25
- 1.2.3. Verificarea ipotezelor statistice 27
- 1.2.4. Modele de analiză grafică 30
- 1.2.5. Gruparea şi clasificarea datelor statistice 31
- 1.2.6. Metode de estimare a parametrilor şi eficacitate a estimaţiilor – metoda celor mai mici pătrate 33
- CAPITOLUL 2 36
- MODELE UTILIZATE ÎN TEORIA TRAGERILOR 36
- 2.1 Parametrii utilizaţi în modelele de optimizare specifice teoriei tragerii 36
- 2.1.1 Forma traiectorie şi însemnătatea ei practică 36
- 2.1.2 Probabilitatea de lovire a obiectivelor 45
- 2.1.3 Fenomenul împrăştierii. Cauzele care produc împrăştierea proiectilelor 46
- 2.1.4 Modele de calcul ale probabilităţii de lovire 48
- 2.2 Modele de optimizare a tragerii asupra obiectivelor mobile 57
- 2.3 Modele de corectare a tragerii în condiţii speciale de presiune şi temperatură 59
- 2.3.1 Influenţa presiunii atmosferice asupra traiectoriei glonţului 59
- 2.3.2 Influenţa temperaturii asupra traiectoriei glonţului. 60
- 2.3.3 Recalcularea probabilităţii de lovire în condiţii speciale de presiune şi temperaturatură 60
- 2.4 Modele de optimizare a tragerii în pantă şi contrapantă 61
- 2.4.1 Recalcularea abaterilor probabile la tragerile în pantă 61
- 2.4.2 Recalcularea abaterilor probabile în contrapantă 63
- 2.5. Economia şi siguranţa tragerii 63
- 2.5.1 Consumul de muniţie 63
- 2.5.2 Aşteptarea matematică 64
- CAPITOLUL 3 66
- UTILIZAREA TEHNICII DE CALCUL ÎN OPTIMIZAREA INSTRUCŢIEI TRAGERII PRIN SIMULAREA MODELELOR STATISTICO-MATEMATICE. PRELUCRĂRI, COLECŢII ŞI VALIDĂRI 66
- 3.1 Aspecte ale utilizării tehnicii de calcul în domeniul militar 66
- 3.2 Programul de simulare la nivel tactic JCATS 67
- 3.3 Etapele procesului de simulare 67
- 3.4 Utilizarea tehnicii de calcul în calcularea elementelor traiectoriei 69
- 3.5 Simularea tragerii asupra obiectivelor mobile 74
- 3.6 Simulare pentru estimarea probabilităţii de lovire şi al consumului de muniţie la tragerea aspura unei ţinte aflată la orice distanţă şi în orice condiţii de presiune şi temperatură 79
- CAPITOLUL 4 88
- PROIECTAREA UNUI SIMULATOR PENTRU EFECTUAREA TRAGERILOR DE PREGĂTIRE ŞI ANTRENAMENT 88
- 4.1 Simulatorul tragere pe bază de laser 88
- 4.2 Proiectarea unui simulator pe bază de laser 92
- CONCLUZII ŞI PROPUNERI 97
- BIBLIOGRAFIE 98
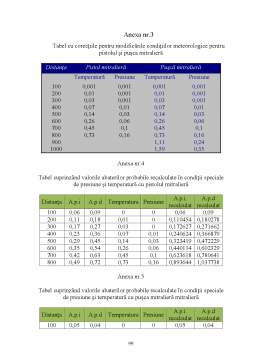
- Anexe 100
Extras din proiect
INTRODUCERE
„Fiecare dintre cele două părţi va căuta să prevadă acţiunea celuilalt, trăgând concluzii din caracterul, instituţiile, situaţia şi condiţiile în care se află adversarul, şi o va adopta pe a sa servindu-se de legile calculului probabilităţilor”
Clausewitz
Suntem martorii unei evoluţii continue a complexităţii mediului militar, asistând totodată la diversificarea problemelor pe care acesta le implică. Deosebit de importante, procesele de pregătire, conducere şi respectiv de asigurare a acţiunilor de luptă se disting prin înglobarea aspectelor cantitative şi calitative ale conţinuturilor lor, aspecte ce se impun a fi studiate în detaliu.
Domeniul militar este caracterizat de întâmpinarea a numeroase situaţii a căror analiză se pretează a fi efectuată cu ajutorul modelelor matematice Aceste situaţii pot fi reprezentate şi studiate cu ajutorul modelelor, cum ar fi de exemplu fenonmenul tragerii cu armamentul de infanterie.
Algoritmii daţi de diferitele tipuri de modele, pe lângă faptul că permit soluţionarea rapidă si uşoară a numeroase probleme din domenii variate de activitate, constituie în acelasi timp procedee eficace de investigaţie ce ajută intuiţia eliminând empirismul şi rutina.
În condiţiile în care informaţia reprezintă putere pe câmpul de luptă modern, cunoaşterea acestor modele este o condiţie esenţială în formarea unor comandanţi care să fie capabili să facă faţă cerinţelor acestuia.
Folosirea metodelor matematice în cunoaşterea şi descrierea fenomenelor reprezintă un pas important spre o treaptă superioară de abstractizare în domeniul militar. Metodele matematice folosite sunt foarte diverse, de la cele clasice, analitice, de tip determinist, la cele nedeterministe ce ţin de teoria probabilităţilor şi proceselor stochastice.
Succesul pe câmpul de luptă presupune o gândire probabilistico-statistică foarte flexibilă, o cunoaştere temeinică a metodelor, modelelor şi tehnicilor pe care le comportă o conducere previzională. Numai aşa putem evita eşecul în faţa inamicului.
Am ales să abordez această temă ca studiu, motivat fiind de pasiunea pentru ştiinţele exacte şi inginereşti, din dorinţa de a studia şi de a înţelege fenomenul tragerii, prin simularea modelelor matematice şi prelucrarea rezultatelor obţinute în urma simulării.
Cunoştinţele de programare şi experienţa în domeniu m-au ajutat în realizarea unor aplicaţii software pe care le-am utilizat în prelucrarea rapidă a rezultatelor, programe care pot fi extrem de utile pentru un comandant de subunitatea mai ales în instrucţia tragerii cu armamentul de infanterie.
Am structurat lucrarea pe 4 capitole, după cum urmează:
Capitolul 1 structurat pe 2 mari subcapitole noţiuni generale de teoria probabilităţilor şi câteva elemente de statistică matematică.
Capitolul 2 prezintă adaptări ale modelelor statistico-matematice la domeniul militar, mai exact adaptări la fenomenul tragerii. Sunt descrişi principalii parametrii, fenomenul împrăştierii loviturilor şi câteva modele utilizate în teoria tragerii.
Capitolul 3 are un caracter practic aplicativ în care am încercat să rezolv câteva probleme legate de fenomenul tragerii prin simularea modelelor prezentate la capitolul 2. Am folosit pentru simularea modelelor câteva aplicaţii soft realizate în limbajul de programare Delphi.
Capitolul 4 este un capitol mai special deoarece încerc să prezint o soluţie de îmbunătăţire a instrucţiei militarilor români, soluţie avantajoasă din toate punctele de vedere, dar mai ales din punct de vedere al economiei de muniţie, timpului instrucţiei şi protecţiei personalului. Am încercat să relizez în măsura posibilităţilor tehnologice pe care le-am avut l-a dispoziţie să relizez un simulator de tragere care să redea cât mai fidel condiţiile reale din poligon. Prezint totodată aici şi posibilităţile de îmbunătăţire ale acestui sistem de simulare.
Am certitudinea că voi atrage atenţia prin această lucrare, mai ales prin simulările pe care le-am realizate şi prin care doresc să încurajez acordarea unei atenţii mai mari simulării în activitatea procesului de instrucţie a militarilor şi bineînţeles acordarea unei atenţii mai mari înţelegerii modelelor statistico-matematice pentru că numai acestea pot apropia simulările de condiţiile reale.
Mulţumesc pe această cale doamnei lect. univ. drd. Cosma Daniela pentru sprijinul acordat în demersul ştiinţific realizat.
CAPITOLUL 1
ELEMENTE DE PROBABILITĂŢI ŞI
STATISTICĂ MATEMATICĂ
1.1. Elemente de teoria probabilităţilor
1.1.1. Definirea termenului de probabilitate
În înţelesul ei cel mai larg, probabilitatea este definită ca măsură a posibilităţii, ca latură cantitativă a întemeierii acesteia. Ea caracterizează nu atât fiinţarea fenomenelor actuale, cât mai ales procesele ce au loc la nivelul acestora, mişcarea şi evoluţia lor; ea este un atribut al existenţei în devenire, al evenimentelor şi nu al lucrurilor.
Fiind expresia cantitativă a întemeierii obiective a perspectivelor de evoluţie a unui sistem, a şanselor acestuia de a trece în altceva, probabilitatea se exprimă matematic printr-o ecuaţie de frecvenţă, ca raport între numărul de cazuri de realizare efectivă a unui eveniment şi numărul total de cazuri posibile.
Formal, matematic, orice eveniment poate fi exprimat în termeni de probabilitate. Evenimentele necesare – caracterizate printr-o concordanţă deplină cu legea fenomenului şi printr-o stabilitate şi concordanţă a condiţiilor de realizare – au o probabilitate egală cu “1”, sau o probabilitate de 100%; evenimentele imposibile au o probabilitate “0”; iar toate celelalte evenimente, care nu sunt necesare sau imposibil, adică evenimentele întâmplătoare, au o probabilitate cuprinsă între “0” şi “1”.
În realitate, nu orice devenire, nu orice eveniment are un caracter probabil. Necesitatea şi imposibilitatea constituie cazuri limită ale variaţiei probabilistice, valoare numerică a raportului probabilistic fiind pentru ele extremă şi constantă; or, ceea ce este constant şi dinainte cunoscut nu poate fi probabil. De aceea, necesitatea şi imposibilitatea nu pot fi considerate fenomene probabile. Descrierea acestora în termeni probabilistici nu aduce nimic nou în înţelegerea lor şi, de aceea, se folosesc în mod curent – în descrierea lor – teorii şi metode matematice neprobabilistice
Probabilitatea este caracteristică fenomenelor lipsite de constanţă şi regularitate, a căror realizare este legată de instabilitatea şi caracterul aleatoriu al apariţiei condiţiilor; ea este deci o caracteristică importantă a fenomenelor întâmplătoare, care comportă o variaţie probabilistică între necesar şi imposibil.
De aceea, probabilitatea este definită drept o dimensiune cantitativă a acestora. Matematic, probabilitatea (P), a unui eveniment întâmplător (A), este redată de expresia 0<P(A)<1.
În cunoaştere, probabilitatea are sens şi valoare numai în cazul fenomenelor întâmplătoare, pentru care există cel puţin două posibilităţi diferite: să se realizeze sau nu, să se realizeze într-o formă sau alta (altfel fenomenul este necesar sau imposibil). Totodată, probabilitatea îşi pierde sensul pentru cunoaştere atunci când fenomenul întâmplător are un număr infinit de posibilităţi, întrucât – deşi evenimentul nu este fizic imposibil – pentru fiecare posibilitate în parte, probabilitatea devine “0”.
Cu toate că probabilitatea este o caracteristică obiectivă a evenimentelor individuale, ea devine evidentă şi capătă o valoare pentru cunoaştere numai atunci când este supus observării un număr mare de evenimente întâmplătoare de acelaşi fel, care se manifestă independent unul de altul. Independenţa reciprocă şi dezordinea evenimentelor individuale dintr-un ansamblu fac ca o anumită proporţie de evenimente din acest ansamblu să se afle în aceeaşi situaţie sau în situaţii asemănătoare, care conduc la acelaşi rezultat (se realizează în acelaşi mod). Acest fenomen poartă denumirea de frecvenţă şi se exprimă prin raportul între numărul cazurilor care se realizează şi numărul total de cazuri posibile. Frecvenţa se realizează la nivelul ansamblului, ca medie statistică a componentelor individuale şi are valoare de necesitate pentru ansamblu; ea este cu atât mai stabilă, cu cât numărul de componente ale ansamblului este mai mare.
Preview document
Conținut arhivă zip
- Studiu cu Privire la Validarea Modelelor Statistico-Matematice de Fundamentare a Deciziilor in Cadrul Misiunilor de Tragere si Indentificarea Corectiilor necesare Compatibilizarii cu Fenomenul Real.doc