Extras din seminar
Fie un Motor de Curent Continuu cu urmatoarele date nominale:
U_An=NRG [V]
R_A=5+NRGmod(5) [Ω]
L_A=10+NRGmod(3) [mH]
(kfi)_n=NRSmod(10)*〖10〗^(-2) [Wb]
J=NRS*〖10〗^(-7) [〖kgm〗^2 ]
F=0
Se cere:
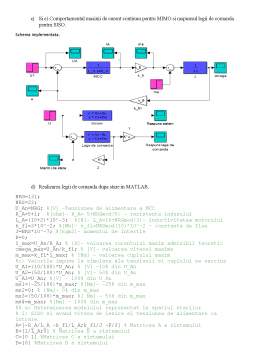
Sa se determine modelul motorului reprezentat in spatial starilor in doua situatii:
Considerand sistemul ca fiind SISO si avand viteza ca iesire si tensiunea de alimentare ca intrare
Considerand sistemul ca fiind MIMO (tensiune si cuplu de sarcina intrari, viteza si cuplul dezvoltat iesiri)
Sa se determine valoarea curentului maxim admisibil teoretic prin masina, precum si valoarea vitezei maxime admisibile teoretice a rotorului.
Sa se simuleze comportamentul masinii pentru tensiunea de alimentare egala cu 10%, 50% si respectiv 100% din valoarea nominala; cuplul de sarcina egal cu -25%, 0%, 50% si respectiv 100% din valoarea maxima, pentru modelul MIMO.
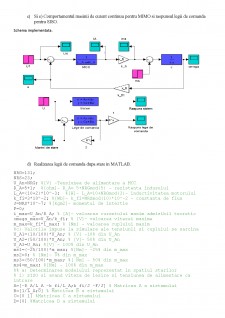
Sa se determine o lege de comanda dupa stare pentru cazul SISO (considerand cuplul de sarcina ca perturbatie si neglijandu-l) stiind ca toate valorile propria impuse sunt egale cu -2.
Sa se simuleze comportamentul sistemului in conditiile de la punctul d) inainte si dupa aplicarea legii de comanda dupa stare pentru cele trei valori ale tensiunii de la punctul c).
Rezolvare:
Datele nominale ale MCC-ului:
U_An=131 [V]
R_A=5+1=7 [Ω]
L_A=10+2=10 [mH]
(kfi)_n=3*〖10〗^(-2) [Wb]
J=23*〖10〗^(-7) [〖kgm〗^2 ]
F=0
Modelarea Motorului de curent continuu in spatiul starilor.
SISO
Sistemul de ecuatii al masinii de curent continuu
u_A=R_A*i+L di/dt+k_fi*Ω /:L
J dΩ/dt=k_fi*i-F*Ω-ms /:J
m_e=k_fi*i
Se separa derivatele de restul termenilor
di/dt=-R/L*i-k_fi/L*Ω+1/L*u_A
dΩ/dt=k_fi/J*i-F/J*Ω-1/J*ms
Se identifica vectorul marimilor de stare, x
x=(i¦Ω) n=2, ordinal matricei A, a sistemului
Identificam marimile de intrare u
u=(u_a¦ms) m=2
Identificarea matricilor A si B din urmatoarea ecuatie
x ̇=Ax+Bu
d/dt (i¦Ω)=(((-R)/L (-k_fi)/L)¦(k_fi/J (-F)/J))(i¦Ω)+((1/L )¦(0 ))(u_A )
A B
Alegem vectorul marimilor de iesire y.Aceasta alegere nu este unica
y=(Ω)
Identificarea matricilor C si D astefel incat avem indeplinita relatia
Preview document
Conținut arhivă zip
- Teoria sistemelor si reglaj automat.docx
Alții au mai descărcat și
1. Definirea pieţei ca spaţiu economic înseamnă că: a) piaţa nu are întotdeauna o determinare geografică; b) piaţa este o confruntare abstractă...
Aplicaţia 1. O pompă transportă un lichid cu densitatea de 960 kg/m3 dintr-un rezervor cu presiunea atmosferică într-un aparat în care presiunea...
De ce mint liderii. Adevărul despre minciunile din politica internațională John J. Mearsheimer Sincer să fiu, am ales această carte deoarece m-a...
Termen Definitie CONSUMATORI Persoana fizica sau grupuri de persoane fizice care nu desfasoara activitati economice OPERATORI ECONOMICI Persoana...
Impactul produs de amenajările hidrotehnice asupra mediului reprezintă o temă complexă dezbătută atăt pe plan intern căt si internaţional. Primele...
LABORATOR Nr. 1 I. Indicaţi pe desen elementele necesare pentru monitorizarea si controlul temperaturii in sala de clasa cu configuraţia din...
1. PRELUCRAREA DOCUMENTELOR Telematica este definită ca fiind tehnica transmiterii la mare distanţă şi valorificării informaţiilor care combină...
Hârtia este un material plan și subțire, având ca element esențial suprafața sa pe care se poate scrie, ale cărei dimensiuni sunt mult mai mari...
Te-ar putea interesa și
1.1 Generalitati Prin automatizarea proceselor de productie se urmareste eliminarea interventiei directe a omului în aceste procese, asigurându-se...
Capitolul 1. Circulaţia feroviară modernă - scurtă caracterizare Transporturile feroviare, deşi afectate uneori de diferite crize circumstanţiale,...
1 Introducere Obiectivul acestei lucrări este studierea unui sistem de reglare automată după stare, aplicat în cadrul unui sistem de laborator,...
Introducere Etapa conducerii complexe a proceselor tehnologice a permis conceperea şi realizarea unor mijloace tehnice care asigură conducerea...
Argument, Structural, un sistem hidraulic automat reprezintă o succesiune de conversii de energie. Motorul electric transformă energia electrică...
INTRODUCERE Maşina asincronă are o pondere importantă în acţionările electrice datorită avantajelor pe care le au comparativ cu alte maşini:...
Partea I-a CONDUCEREA PROCESELOR DUPA MARIMEA DE IESIRE 1. Structuri de baza si metode de proiectare 1.1. Structuri de reglare si metode de...
Introducere în “Calitate” si “Managementul calitatii” 1.1. Prezentare generala a problemei calitatii Pe masura ce tehnologiile evolueaza, oferta...