Cuprins
- Introducere ȋn algebra booleanǎ 2
- 1. Algebra Booleanǎ 2
- 2. Proprietǎțile algebrei booleene 2
- • idempotența 2
- • comutativitatea 2
- • asociativitatea 2
- • distributivitatea 2
- • simetria 3
- • reflexivitatea 3
- • tranzitivitatea 3
- • Teoremele lui De Morgan 3
- • Teoreme de absorbție (utile pentru simplificarea expresiilor logice): 3
- • Alte relații 3
- 3. Reprezentarea funcțiilor logice 3
- • Prin tabele de adevǎr 3
- • Ȋn formǎ algebricǎ prin: 3
- • Forma normală disjunctivă (FND) (sumǎ/disjuncție de produse/conjuncții) 3
- • Forma normală conjunctivă (FNC) (produse/conjuncții de suma/disjuncții) 3
- • Prin ∑ - notație 4
- 4. Minimizarea funcțiilor logice 4
- • Prin metoda algebricǎ 4
- • Prin metoda diagramelor Karnaugh 5
- 5. Porți logice 5
- 6. Implementarea funcțiilor logice 7
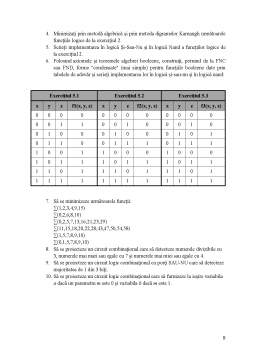
- 7. Exerciții 7
Extras din seminar
Introducere ȋn algebra booleanǎ
1. Algebra Booleanǎ
- Se mai numește și logicǎ booleanǎ;
- Și-a cǎpǎtat numele dupǎ matematicianul englez George Boole, care a scris despre ea ȋn cartea sa „O investigare a legilor gȃndirii” („An investigation of the Laws of Thought”) - 1854;
- Printre aplicațiile algebrei logice se numǎrǎ: logica matematicǎ, logica digitalǎ, programarea calculatoarelor, statistica;
- Cel care a descoperit aplicabilitatea algebrei booleene ȋn electronicǎ este Shannon Claude Elwood, el demonstrȃnd ȋn teza de absolvire a masteratului cǎ orice problemǎ de logicǎ se poate rezolva utilizȃnd relee;
- O funcție logicǎ (funcție booleanǎ) este de tipul:
- Operatorii logici de bazǎ sunt:
Operator: ȘI SAU NU
Notație * +
Denumire alternatvǎ Produs logic
Conjuncție Sumǎ logicǎ
Disjuncție
- Prin combinația celor 3 se obțin restul operatorilor: Sau exclusiv (XOR), Sau negat (NOR), Și negat(NAND)
2. Proprietǎțile algebrei booleene
• idempotența
o a + a = a
0 + 0 = 0
1 + 1 = 1
o a ∙ a = a
0 ∙ 0 = 0
1 ∙ 1 = 1
• comutativitatea
a + b = b + a
a ∙ b = b ∙ a
• asociativitatea
(a + b) + c = a + ( b + c ) = a + b + c
(a ∙ b) ∙ c = a ∙ ( b ∙ c ) = a ∙ b ∙ c
• distributivitatea
a ∙ ( b + c ) = a ∙ b + a ∙ c
• simetria
a = b → b = a
• reflexivitatea
a = a
• tranzitivitatea
→ a = c
• Teoremele lui De Morgan
1.
2.
• Teoreme de absorbție (utile pentru simplificarea expresiilor logice):
1. + =
2. a
3. a + = a + b
4. a = a b
5. a + c + b c = a b + c
6. (a + b) ( + c) (b + c) = (a + b) ( + c)
• Alte relații
+ 0 =
+ 1 = 1
∙ 0 = 0
∙ 1 =
+ = 1
∙ = 0
=
3. Reprezentarea funcțiilor logice
• Prin tabele de adevǎr
• Ȋn formǎ algebricǎ prin:
• Forma normală disjunctivă (FND) (sumǎ/disjuncție de produse/conjuncții)
• Forma normală conjunctivă (FNC) (produse/conjuncții de suma/disjuncții)
Preview document
Conținut arhivă zip
- Algebra Booleana.doc